- {x}
- Top K Frequent Words
- Binary Number with Alternating Bits
- Number of Distinct Islands
- Max Area of Island
- Count Binary Substrings
- Degree of an Array
- Partition to K Equal Sum Subsets
- Falling Squares
- Search in a Binary Search Tree
- Insert into a Binary Search Tree
- Search in a Sorted Array of Unknown Size
- Kth Largest Element in a Stream
- Binary Search
- Design HashSet
- Design HashMap
- Design Linked List
- Insert into a Sorted Circular Linked List
- Read More...

Search in a Binary Search Tree
You are given the root of a binary search tree (BST) and an integer val.
Find the node in the BST that the node's value equals val and return the subtree rooted with that node. If such a node does not exist, return null.
Example 1:
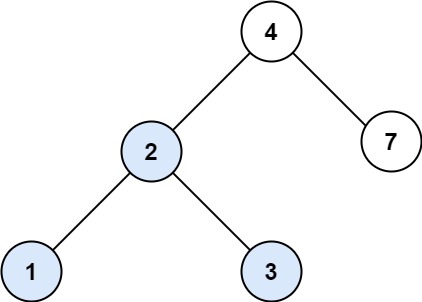
Input: root = [4,2,7,1,3], val = 2 Output: [2,1,3]
Example 2:
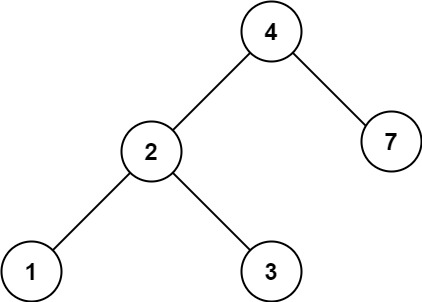
Input: root = [4,2,7,1,3], val = 5 Output: []
Constraints:
- The number of nodes in the tree is in the range
[1, 5000]. 1 <= Node.val <= 107rootis a binary search tree.1 <= val <= 107
Solution Explanation: Searching in a Binary Search Tree
This problem involves finding a node with a specific value (val) within a Binary Search Tree (BST). The key to efficiently solving this is leveraging the inherent property of a BST: nodes in the left subtree are smaller than the current node, and nodes in the right subtree are larger.
Approach
The most efficient approach is a recursive search. We start at the root of the BST. We compare the root's value to val:
-
Base Cases:
- If the root is
null(empty tree), the value is not found, so returnnull. - If the root's value equals
val, the node is found, so return the root.
- If the root is
-
Recursive Step:
- If the root's value is greater than
val, the target node (if it exists) must be in the left subtree. Recursively call thesearchBSTfunction on the left subtree. - If the root's value is less than
val, the target node must be in the right subtree. Recursively call thesearchBSTfunction on the right subtree.
- If the root's value is greater than
Time and Space Complexity Analysis
-
Time Complexity: O(H), where H is the height of the BST. In the worst case (a skewed tree), H could be equal to N (the number of nodes), resulting in O(N) time complexity. However, in a balanced BST, H is log₂(N), giving us O(log N) time complexity, which is significantly more efficient.
-
Space Complexity: O(H) in the worst case due to the recursive call stack. Again, this translates to O(N) for a skewed tree and O(log N) for a balanced tree.
Code Implementation (Python)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
if not root or root.val == val: # Base cases: empty tree or found
return root
elif root.val > val: # Search left subtree
return self.searchBST(root.left, val)
else: # Search right subtree
return self.searchBST(root.right, val)The code in other languages (Java, C++, Go, TypeScript) follows the same recursive logic, differing only in syntax. The core algorithm remains consistent. The iterative approach (using a while loop instead of recursion) would have the same time complexity but a slightly better space complexity of O(1) because it avoids the recursive call stack. However, the recursive approach is often considered more readable and concise.