- {x}
- Warehouse Manager
- Matrix Diagonal Sum
- Number of Ways to Split a String
- Shortest Subarray to be Removed to Make Array Sorted
- Count All Possible Routes
- Replace All ?'s to Avoid Consecutive Repeating Characters
- Number of Ways Where Square of Number Is Equal to Product of Two Numbers
- Minimum Time to Make Rope Colorful
- Remove Max Number of Edges to Keep Graph Fully Traversable
- Put Boxes Into the Warehouse II
- Customer Who Visited but Did Not Make Any Transactions
- Special Positions in a Binary Matrix
- Count Unhappy Friends
- Min Cost to Connect All Points
- Check If String Is Transformable With Substring Sort Operations
- Binary Search Tree Iterator II
- Bank Account Summary II
- Read More...

Remove Max Number of Edges to Keep Graph Fully Traversable
Alice and Bob have an undirected graph of n nodes and three types of edges:
- Type 1: Can be traversed by Alice only.
- Type 2: Can be traversed by Bob only.
- Type 3: Can be traversed by both Alice and Bob.
Given an array edges where edges[i] = [typei, ui, vi] represents a bidirectional edge of type typei between nodes ui and vi, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return the maximum number of edges you can remove, or return -1 if Alice and Bob cannot fully traverse the graph.
Example 1:
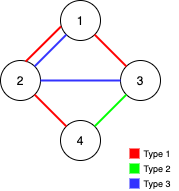
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]] Output: 2 Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
Example 2:
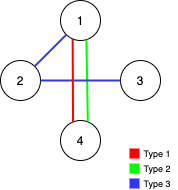
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]] Output: 0 Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
Example 3:
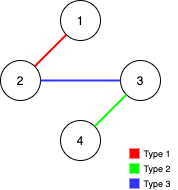
Input: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]] Output: -1 Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
Constraints:
1 <= n <= 1051 <= edges.length <= min(105, 3 * n * (n - 1) / 2)edges[i].length == 31 <= typei <= 31 <= ui < vi <= n- All tuples
(typei, ui, vi)are distinct.
Solution Explanation
This problem involves finding the maximum number of edges that can be removed from a graph while ensuring that both Alice and Bob can still traverse the entire graph. The graph has three types of edges: type 1 (Alice only), type 2 (Bob only), and type 3 (both Alice and Bob).
The solution uses the Union-Find data structure to efficiently determine connectivity. The approach is as follows:
-
Initialization: Two Union-Find structures,
ufaandufb, are created.ufatracks connectivity for Alice, andufbtracks connectivity for Bob. -
Processing Type 3 Edges: The algorithm first iterates through edges of type 3. These edges can be used by both Alice and Bob. If adding a type 3 edge connects two previously disconnected components in both
ufaandufb, it's added; otherwise, it's considered removable and the counteransis incremented. -
Processing Type 1 and Type 2 Edges: Next, the algorithm processes type 1 and type 2 edges separately. For each edge, it attempts to add it to the appropriate Union-Find structure (
ufafor type 1,ufbfor type 2). If adding the edge fails (meaning the nodes are already connected), the edge is considered removable, andansis incremented. -
Connectivity Check: After processing all edges, the algorithm checks if both
ufaandufbhave only one connected component (ufa.cnt == 1 && ufb.cnt == 1). If not, it means either Alice or Bob cannot traverse the entire graph, and -1 is returned. Otherwise,ans(the number of removable edges) is returned.
Time Complexity Analysis
The time complexity is dominated by the iterations through the edges and the Union-Find operations. Union-Find operations (find and union) have an amortized time complexity of O(α(n)), where α(n) is the inverse Ackermann function, which grows extremely slowly and can be considered practically constant for all realistic input sizes. Therefore, the overall time complexity is O(M + N) where M is the number of edges and N is the number of nodes. This is linear with respect to the input size.
Space Complexity Analysis
The space complexity is dominated by the Union-Find data structures. Each Union-Find structure uses O(N) space to store its parent array and size array. Therefore, the overall space complexity is O(N), linear with respect to the number of nodes.
Code Examples (Python3, Java, C++, Go)
The code examples provided in the previous response demonstrate the implementation of this solution in Python3, Java, C++, and Go. Each example includes a UnionFind class implementing the Union-Find algorithm, which is then used in the maxNumEdgesToRemove function to solve the problem as described above. Refer to those code examples for a complete and detailed implementation.