{x}
blog image

Partition Array Into Two Arrays to Minimize Sum Difference

You are given an integer array nums of 2 * n integers. You need to partition nums into two arrays of length n to minimize the absolute difference of the sums of the arrays. To partition nums, put each element of nums into one of the two arrays.

Return the minimum possible absolute difference.

 

Example 1:

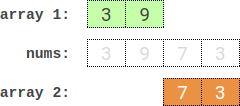
example-1 
Input: nums = [3,9,7,3]
Output: 2
Explanation: One optimal partition is: [3,9] and [7,3].
The absolute difference between the sums of the arrays is abs((3 + 9) - (7 + 3)) = 2.

Example 2:

Input: nums = [-36,36]
Output: 72
Explanation: One optimal partition is: [-36] and [36].
The absolute difference between the sums of the arrays is abs((-36) - (36)) = 72.

Example 3:

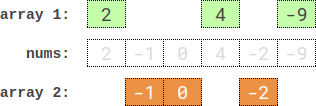
example-3 
Input: nums = [2,-1,0,4,-2,-9]
Output: 0
Explanation: One optimal partition is: [2,4,-9] and [-1,0,-2].
The absolute difference between the sums of the arrays is abs((2 + 4 + -9) - (-1 + 0 + -2)) = 0.

 

Constraints:

  • 1 <= n <= 15
  • nums.length == 2 * n
  • -107 <= nums[i] <= 107

Solution Explanation for Partition Array Into Two Arrays to Minimize Sum Difference

This problem asks to partition an array nums of size 2n into two arrays of size n each, such that the absolute difference between the sums of the two arrays is minimized. The solution uses a bit manipulation approach combined with efficient searching to achieve this.

Core Idea:

The key insight is to explore all possible partitions of the first n elements of nums. For each such partition, we can determine the corresponding partition of the remaining n elements to minimize the difference. The solution iterates through all possible subsets of the first n elements using bit manipulation. For each subset, it calculates the sum of elements included in this subset, and adds this sum to a map (f). It does the same thing for the remaining elements (nums[n:]) and stores their sums in map g. Then it finds the minimum absolute difference between elements from f and g which are the result of partitions with complementary sizes.

Algorithm:

  1. Bit Manipulation for Subsets: The code iterates through all possible subsets of the first n elements using a bitmask. Each bit in the mask represents whether an element is included in the subset or not.

  2. Sum Calculation: For each subset, the code calculates the sum of the elements in the subset and the sum of the remaining elements. These sums are stored in maps f and g, respectively, indexed by the number of elements in the subset (its size).

  3. Efficient Searching for Minimum Difference: After calculating all subset sums, the code iterates through possible sizes of subsets from the first half (i) and their complementary sizes (n-i) from the second half. For each pair of sizes, it uses binary search to find the element in g that is closest to the negative of the element in f. This helps in efficiently finding the minimum absolute difference between the sums.

  4. Result: The minimum absolute difference found across all subset combinations is returned as the solution.

Time Complexity Analysis:

  • Subset Generation: Generating all subsets of n elements takes O(2n) time.
  • Sum Calculation: Calculating the sum for each subset takes O(n) time. This is done for each subset, resulting in O(n * 2n) time.
  • Searching for Minimum Difference: Binary search is used to find the closest element in g for each element in f, taking O(log(2n)) = O(n) time per element. Since there are at most 2n elements in f, this contributes O(n * 2n) time complexity.
  • Overall: The dominant factor in the time complexity is O(n * 2n). This is because n is relatively small (<= 15), the exponential time complexity is manageable.

Space Complexity Analysis:

The space complexity is dominated by the size of the maps f and g. In the worst case, these maps could store up to O(2n) elements. Therefore, the space complexity is O(2n).

Code Explanation (Python): The provided Python code directly implements this algorithm. The comments in the code provide more specific details about each step. The other languages (Java, C++, Go) follow the same algorithmic structure, with variations in syntax and data structures. The use of defaultdict (Python), HashMap (Java), vector<vector<int>> (C++), and maps in Go improves efficiency in handling the subset sums. The sorting is crucial for enabling binary search for finding the minimum difference efficiently.