{x}
blog image

Pacific Atlantic Water Flow

There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.

The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).

The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.

Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.

 

Example 1:

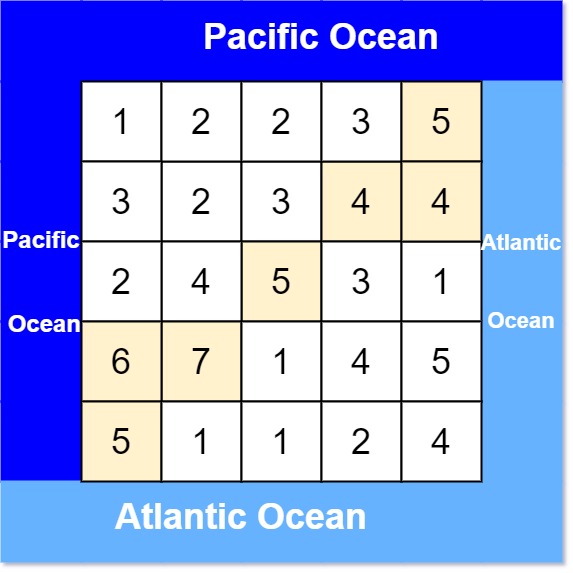
Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans, as shown below:
[0,4]: [0,4] -> Pacific Ocean 
       [0,4] -> Atlantic Ocean
[1,3]: [1,3] -> [0,3] -> Pacific Ocean 
       [1,3] -> [1,4] -> Atlantic Ocean
[1,4]: [1,4] -> [1,3] -> [0,3] -> Pacific Ocean 
       [1,4] -> Atlantic Ocean
[2,2]: [2,2] -> [1,2] -> [0,2] -> Pacific Ocean 
       [2,2] -> [2,3] -> [2,4] -> Atlantic Ocean
[3,0]: [3,0] -> Pacific Ocean 
       [3,0] -> [4,0] -> Atlantic Ocean
[3,1]: [3,1] -> [3,0] -> Pacific Ocean 
       [3,1] -> [4,1] -> Atlantic Ocean
[4,0]: [4,0] -> Pacific Ocean 
       [4,0] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.

Example 2:

Input: heights = [[1]]
Output: [[0,0]]
Explanation: The water can flow from the only cell to the Pacific and Atlantic oceans.

 

Constraints:

  • m == heights.length
  • n == heights[r].length
  • 1 <= m, n <= 200
  • 0 <= heights[r][c] <= 105

Solution Explanation:

This problem asks to find all cells in a matrix that can flow to both the Pacific and Atlantic oceans. Water can flow from a cell to its adjacent cell if the adjacent cell's height is less than or equal to the current cell's height. The Pacific Ocean touches the left and top edges, and the Atlantic Ocean touches the right and bottom edges.

The most efficient approach uses Breadth-First Search (BFS) or Depth-First Search (DFS). We perform two separate searches: one starting from the Pacific Ocean's border and another from the Atlantic Ocean's border.

Algorithm:

  1. Initialization:

    • Create two sets, pacificReachable and atlanticReachable, to store cells reachable from the Pacific and Atlantic oceans, respectively.
    • Create two queues, pacificQueue and atlanticQueue, for BFS. Initialize them with cells bordering the respective oceans.

  2. BFS (for Pacific):

    • While pacificQueue is not empty:
      • Dequeue a cell (row, col).
      • For each adjacent cell (newRow, newCol):
        • If (newRow, newCol) is within bounds, not already in pacificReachable, and its height is less than or equal to the current cell's height, add it to pacificReachable and pacificQueue.

  3. BFS (for Atlantic): Repeat step 2 for the Atlantic Ocean.

  4. Find Common Cells: Iterate through the matrix. If a cell is present in both pacificReachable and atlanticReachable, add its coordinates to the result list.

Time Complexity: O(M*N), where M and N are the dimensions of the matrix. We visit each cell at most once in each BFS.

Space Complexity: O(M*N) in the worst case, to store the pacificReachable and atlanticReachable sets and the queues.

Code Explanation (Python):

from collections import deque
 
def pacificAtlantic(heights):
    rows, cols = len(heights), len(heights[0])
    pacificReachable = set()
    atlanticReachable = set()
    pacificQueue = deque()
    atlanticQueue = deque()
 
    # Add border cells to queues
    for r in range(rows):
        pacificQueue.append((r, 0))  # Left border
        atlanticQueue.append((r, cols - 1))  # Right border
    for c in range(cols):
        pacificQueue.append((0, c))  # Top border
        atlanticQueue.append((rows - 1, c))  # Bottom border
 
    # BFS for Pacific
    while pacificQueue:
        row, col = pacificQueue.popleft()
        pacificReachable.add((row, col))
        for dr, dc in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
            newRow, newCol = row + dr, col + dc
            if (0 <= newRow < rows and 0 <= newCol < cols and
                    (newRow, newCol) not in pacificReachable and
                    heights[newRow][newCol] >= heights[row][col]):
                pacificQueue.append((newRow, newCol))
 
    # BFS for Atlantic
    while atlanticQueue:
        row, col = atlanticQueue.popleft()
        atlanticReachable.add((row, col))
        for dr, dc in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
            newRow, newCol = row + dr, col + dc
            if (0 <= newRow < rows and 0 <= newCol < cols and
                    (newRow, newCol) not in atlanticReachable and
                    heights[newRow][newCol] >= heights[row][col]):
                atlanticQueue.append((newRow, newCol))
    
    # Find common cells
    result = []
    for r in range(rows):
        for c in range(cols):
            if (r, c) in pacificReachable and (r, c) in atlanticReachable:
                result.append([r, c])
    return result

The other languages (Java, C++, Go, TypeScript) follow a very similar structure, adapting the data structures and syntax accordingly. The core algorithm remains the same.