- {x}
- Maximum Number of Coins You Can Get
- Find Latest Group of Size M
- Stone Game V
- Put Boxes Into the Warehouse I
- Unique Orders and Customers Per Month
- Detect Pattern of Length M Repeated K or More Times
- Maximum Length of Subarray With Positive Product
- Minimum Number of Days to Disconnect Island
- Number of Ways to Reorder Array to Get Same BST
- Dot Product of Two Sparse Vectors
- Warehouse Manager
- Matrix Diagonal Sum
- Number of Ways to Split a String
- Shortest Subarray to be Removed to Make Array Sorted
- Count All Possible Routes
- Replace All ?'s to Avoid Consecutive Repeating Characters
- Number of Ways Where Square of Number Is Equal to Product of Two Numbers
- Read More...

Number of Ways to Reorder Array to Get Same BST
Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.
- For example, given
nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array[2,3,1]also yields the same BST but[3,2,1]yields a different BST.
Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.
Since the answer may be very large, return it modulo 109 + 7.
Example 1:
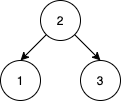
Input: nums = [2,1,3] Output: 1 Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
Example 2:
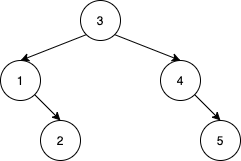
Input: nums = [3,4,5,1,2] Output: 5 Explanation: The following 5 arrays will yield the same BST: [3,1,2,4,5] [3,1,4,2,5] [3,1,4,5,2] [3,4,1,2,5] [3,4,1,5,2]
Example 3:
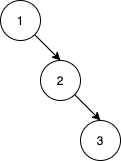
Input: nums = [1,2,3] Output: 0 Explanation: There are no other orderings of nums that will yield the same BST.
Constraints:
1 <= nums.length <= 10001 <= nums[i] <= nums.length- All integers in
numsare distinct.
1569. Number of Ways to Reorder Array to Get Same BST
Problem Description
Given an array nums representing a permutation of integers from 1 to n, construct a Binary Search Tree (BST) by inserting elements of nums in order. The task is to find the number of different ways to reorder nums such that the constructed BST remains identical to the one formed from the original array. The answer might be large, so it should be returned modulo 109 + 7.
Solution: Combination Counting + Recursion
This problem can be efficiently solved using a recursive approach combined with combinatorial calculations. The core idea is to leverage the properties of BSTs:
- Root: The first element in any valid ordering will always be the root of the BST.
- Subtrees: Elements smaller than the root form the left subtree, and elements larger than the root form the right subtree. These subtrees are independent BSTs themselves.
The recursive function dfs(nums) calculates the number of ways to reorder the input array nums such that the resulting BST is identical.
- Base Case: If
numshas fewer than 2 elements, there's only 1 way (itself). - Recursive Step:
- Partition
numsintoleft(elements < root) andright(elements > root). - Recursively calculate the number of ways for
leftandrightsubtrees:a = dfs(left)andb = dfs(right). - The total number of ways is the product of:
- The number of ways to arrange elements in the left and right subtrees (
a * b). - The number of ways to choose positions for the left subtree elements among all the elements (excluding the root). This is given by the binomial coefficient
C(m+n, m), wheremis the size ofleftandnis the size ofright. This coefficient represents the number of ways to choosempositions out ofm+ntotal positions.
- The number of ways to arrange elements in the left and right subtrees (
- Partition
The binomial coefficient C(m+n, m) is pre-calculated using Pascal's triangle to improve efficiency. We use dynamic programming to compute these coefficients, avoiding redundant computations.
Finally, the result is dfs(nums) - 1 (because the original ordering is already counted), taken modulo 109 + 7.
Time and Space Complexity
- Time Complexity: O(n2) due to the recursive nature of the
dfsfunction and the pre-computation of binomial coefficients. The recursion explores all possible combinations. - Space Complexity: O(n2) primarily due to the storage of pre-computed binomial coefficients. The recursion depth can also reach O(n) in the worst case (a skewed BST).
Code (Python)
class Solution:
def numOfWays(self, nums: List[int]) -> int:
n = len(nums)
mod = 10**9 + 7
c = [[0] * n for _ in range(n)]
c[0][0] = 1
for i in range(1, n):
c[i][0] = 1
for j in range(1, i + 1):
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod
def dfs(nums):
if len(nums) < 2:
return 1
left = [x for x in nums if x < nums[0]]
right = [x for x in nums if x > nums[0]]
m, n = len(left), len(right)
a, b = dfs(left), dfs(right)
return (((c[m + n][m] * a) % mod) * b) % mod
return (dfs(nums) - 1 + mod) % modThe code in other languages (Java, C++, Go, TypeScript) follows a very similar structure, with the main differences lying in syntax and data structure handling. The core logic of recursion and binomial coefficient calculation remains consistent across all implementations.