- {x}
- Kill Process
- Delete Operation for Two Strings
- Find Customer Referee
- Investments in 2016
- Customer Placing the Largest Number of Orders
- Erect the Fence
- Design In-Memory File System
- N-ary Tree Preorder Traversal
- N-ary Tree Postorder Traversal
- Tag Validator
- Fraction Addition and Subtraction
- Valid Square
- Longest Harmonious Subsequence
- Big Countries
- Classes More Than 5 Students
- Friend Requests I: Overall Acceptance Rate
- Range Addition II
- Read More...

N-ary Tree Postorder Traversal
Given the root of an n-ary tree, return the postorder traversal of its nodes' values.
Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)
Example 1:
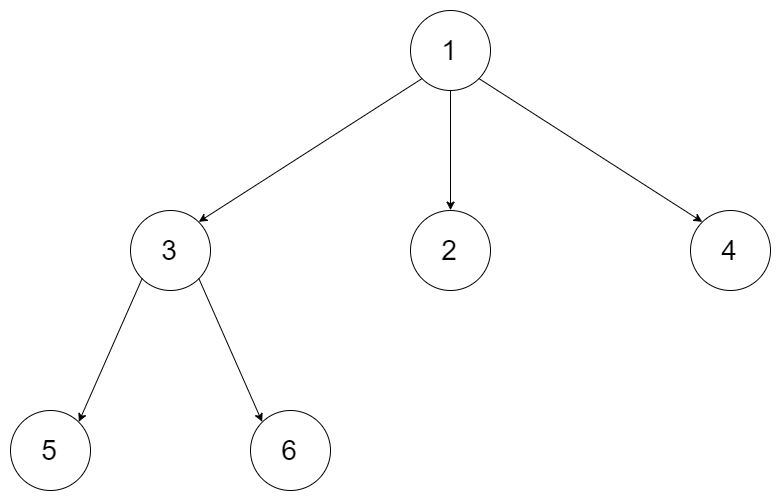
Input: root = [1,null,3,2,4,null,5,6] Output: [5,6,3,2,4,1]
Example 2:
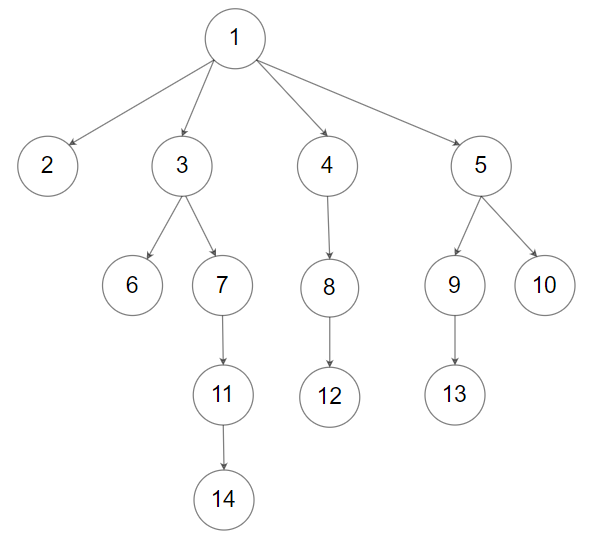
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] Output: [2,6,14,11,7,3,12,8,4,13,9,10,5,1]
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. 0 <= Node.val <= 104- The height of the n-ary tree is less than or equal to
1000.
Follow up: Recursive solution is trivial, could you do it iteratively?
590. N-ary Tree Postorder Traversal
This problem asks for a postorder traversal of an N-ary tree. Postorder traversal means visiting the nodes in the order of: left subtree, right subtree, ..., root. In an N-ary tree, "left" and "right" generalize to all children.
Solutions
Two approaches are presented: recursion and iteration.
Solution 1: Recursion
This is the most straightforward approach for tree traversal. The recursive function dfs performs the following steps:
- Base Case: If the node is
null, it returns. - Recursive Calls: It recursively calls
dfson each of the node's children. - Append to Result: After processing all children, it appends the current node's value to the
anslist.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited exactly once.
Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be N.
class Solution:
def postorder(self, root: 'Node') -> List[int]:
ans = []
def dfs(root):
if root is None:
return
for child in root.children:
dfs(child)
ans.append(root.val)
dfs(root)
return ansOther languages (Java, C++, Go, TypeScript) follow a very similar recursive structure.
Solution 2: Iteration (using Stack)
This iterative approach uses a stack to simulate the recursive calls.
- Initialization: It starts with a stack containing the root node.
- Iteration: While the stack is not empty:
- It pops the top node from the stack.
- It appends the node's value to the
anslist. Crucially, this happens after processing the children. - It pushes the node's children onto the stack (in reverse order to maintain the postorder sequence).
- Reversal (Python): In Python, since we are appending to the beginning of
ans, we need to reverse the list at the end to get the correct postorder sequence. Other languages might directly prepend to get the correct order.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited and processed once.
Space Complexity: O(N), where N is the number of nodes. In the worst-case scenario (a completely unbalanced tree), the stack could hold all nodes.
class Solution:
def postorder(self, root: 'Node') -> List[int]:
ans = []
if root is None:
return ans
stk = [root]
while stk:
node = stk.pop()
ans.append(node.val)
for child in node.children:
stk.append(child)
return ans[::-1] # Reverse for PythonThe iterative solutions in other languages (Java, C++, Go, TypeScript) are similar, but might handle the order of appending differently (e.g., using a LinkedList in Java to directly prepend, thereby avoiding the final reversal step). The core principle—using a stack to mimic recursion—remains consistent across all languages.