- {x}
- Maximum XOR of Two Numbers in an Array
- Valid Word Square
- Reconstruct Original Digits from English
- Longest Repeating Character Replacement
- Word Squares
- Convert Binary Search Tree to Sorted Doubly Linked List
- Construct Quad Tree
- Serialize and Deserialize N-ary Tree
- N-ary Tree Level Order Traversal
- Flatten a Multilevel Doubly Linked List
- Encode N-ary Tree to Binary Tree
- All O`one Data Structure
- Minimum Genetic Mutation
- Number of Segments in a String
- Non-overlapping Intervals
- Find Right Interval
- Path Sum III
- Read More...

N-ary Tree Level Order Traversal
Given an n-ary tree, return the level order traversal of its nodes' values.
Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).
Example 1:
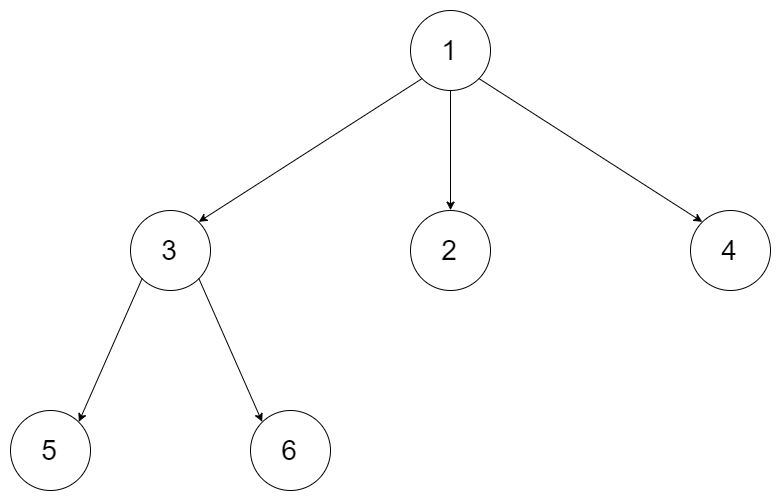
Input: root = [1,null,3,2,4,null,5,6] Output: [[1],[3,2,4],[5,6]]
Example 2:
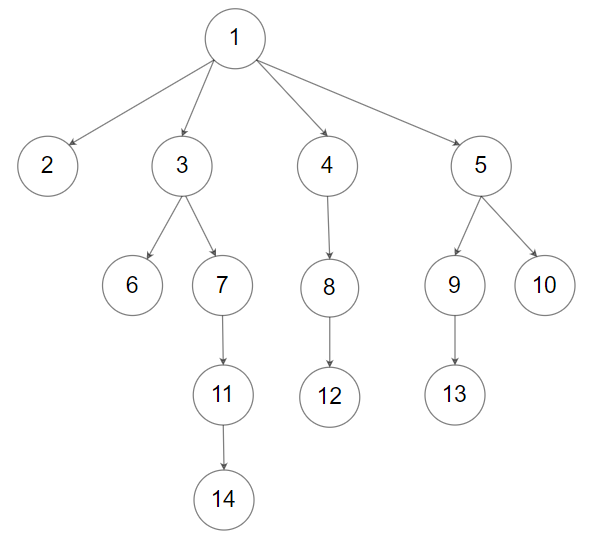
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] Output: [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
Constraints:
- The height of the n-ary tree is less than or equal to
1000 - The total number of nodes is between
[0, 104]
429. N-ary Tree Level Order Traversal
This problem asks for a level order traversal of an N-ary tree. Level order traversal means visiting all nodes at a given level before moving to the next level. Because of the tree's structure, Breadth-First Search (BFS) is the natural approach. Depth-First Search (DFS) can also be adapted, but BFS is generally more efficient for level order traversal.
Approach 1: Breadth-First Search (BFS)
BFS uses a queue to systematically explore the tree level by level.
Algorithm:
-
Initialization:
- Create an empty list
ansto store the level order traversal result (a list of lists, where each inner list represents a level). - Create a queue
qand add the root node to it. If the root isnull, return an empty list.
- Create an empty list
-
Iteration:
- While the queue
qis not empty:- Create an empty list
levelto store the values of nodes at the current level. - Get the size
nof the queue (the number of nodes at the current level). - Iterate
ntimes:- Dequeue a node from
q. - Add the node's value to the
levellist. - Enqueue all the children of the dequeued node into
q.
- Dequeue a node from
- Add the
levellist toans.
- Create an empty list
- While the queue
-
Return:
- Return the
anslist.
- Return the
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited and processed exactly once.
Space Complexity: O(W), where W is the maximum width (number of nodes) at any level of the tree. In the worst case (a complete tree), W can be proportional to N.
Code (Python):
from collections import deque
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
ans = []
if not root:
return ans
q = deque([root])
while q:
level = []
for _ in range(len(q)):
node = q.popleft()
level.append(node.val)
q.extend(node.children)
ans.append(level)
return ans
Code (Java):
import java.util.*;
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> ans = new ArrayList<>();
if (root == null) return ans;
Queue<Node> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
List<Integer> level = new ArrayList<>();
int n = q.size();
for (int i = 0; i < n; i++) {
Node node = q.poll();
level.add(node.val);
if (node.children != null) q.addAll(node.children);
}
ans.add(level);
}
return ans;
}
}Approach 2: Depth-First Search (DFS) with Level Tracking
While BFS is more natural for level order traversal, DFS can also be adapted. We need to track the current level during the traversal.
Algorithm:
-
Initialization:
- Create an empty list
ansto store the result. - Define a recursive helper function
dfs(node, level).
- Create an empty list
-
DFS Helper Function:
- Base Case: If
nodeisnull, return. - If the
levelis greater than or equal to the size ofans, append a new empty list toans. - Add the node's value to
ans[level]. - Recursively call
dfsfor each child, incrementing thelevel.
- Base Case: If
-
Main Function:
- Call
dfs(root, 0)to start the traversal. - Return
ans.
- Call
Time Complexity: O(N), same as BFS.
Space Complexity: O(H), where H is the height of the tree. The space usage is dominated by the recursion stack, whose depth is at most H. In the worst case (a skewed tree), H can be N.
Code (Python):
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
ans = []
def dfs(node, level):
if not node:
return
if level >= len(ans):
ans.append([])
ans[level].append(node.val)
for child in node.children:
dfs(child, level + 1)
dfs(root, 0)
return ansBoth BFS and DFS solutions have the same time complexity, but BFS generally uses less space for level order traversal, especially for wider trees. Choose BFS for better space efficiency in most cases.