- {x}
- Design a Text Editor
- Jump Game VIII
- Tasks Count in the Weekend
- Strong Password Checker II
- Successful Pairs of Spells and Potions
- Match Substring After Replacement
- Count Subarrays With Score Less Than K
- Calculate Amount Paid in Taxes
- Minimum Path Cost in a Grid
- Fair Distribution of Cookies
- Naming a Company
- Check for Contradictions in Equations
- Arrange Table by Gender
- Greatest English Letter in Upper and Lower Case
- Sum of Numbers With Units Digit K
- Longest Binary Subsequence Less Than or Equal to K
- Selling Pieces of Wood
- Read More...

Minimum Path Cost in a Grid
You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1). Note that it is not possible to move from cells in the last row.
Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.
The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.
Example 1:
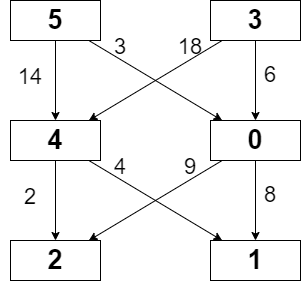
Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]] Output: 17 Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1. - The sum of the values of cells visited is 5 + 0 + 1 = 6. - The cost of moving from 5 to 0 is 3. - The cost of moving from 0 to 1 is 8. So the total cost of the path is 6 + 3 + 8 = 17.
Example 2:
Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]] Output: 6 Explanation: The path with the minimum possible cost is the path 2 -> 3. - The sum of the values of cells visited is 2 + 3 = 5. - The cost of moving from 2 to 3 is 1. So the total cost of this path is 5 + 1 = 6.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 50gridconsists of distinct integers from0tom * n - 1.moveCost.length == m * nmoveCost[i].length == n1 <= moveCost[i][j] <= 100
Minimum Path Cost in a Grid
This problem asks to find the minimum cost path from the top row to the bottom row of a grid, where the cost is the sum of the cell values and the movement costs between cells. We can efficiently solve this using dynamic programming.
Approach:
The dynamic programming approach builds a solution from subproblems. We'll use a DP table (or array in the optimized version) to store the minimum cost to reach each cell.
-
Initialization: The minimum cost to reach any cell in the first row is simply the value of that cell.
-
Iteration: For each subsequent row, we calculate the minimum cost to reach each cell in that row. To reach a cell
(i, j), we consider all possible cells(i-1, k)in the previous row (where0 <= k < n) and calculate the cost of moving from(i-1, k)to(i, j). This cost consists of:- The minimum cost to reach
(i-1, k)(obtained from our DP table). - The movement cost from
grid[i-1][k]to columnj(obtained frommoveCost). - The value of the current cell
grid[i][j].
We choose the minimum cost among all possible
kvalues. - The minimum cost to reach
-
Result: The minimum cost to reach the bottom row is the minimum value in the last row of our DP table.
Optimization:
Since we only need the information from the previous row to compute the current row's minimum costs, we can optimize space complexity by using only two arrays to store the minimum cost for the current row and previous row instead of a full DP table.
Time and Space Complexity:
-
Time Complexity: O(m * n^2), where 'm' is the number of rows and 'n' is the number of columns in the grid. This is because for each cell in rows 1 to m-1, we iterate through all n cells in the previous row to find the minimum cost.
-
Space Complexity: O(n) in the optimized version (using two arrays to represent rows), as opposed to O(m*n) for the non-optimized version which uses a complete DP table.
Code Implementation:
Here are implementations in several programming languages:
Python:
import sys
def minPathCost(grid, moveCost):
m, n = len(grid), len(grid[0])
prev_row = grid[0] # Initialize with the first row
for i in range(1, m):
curr_row = [sys.maxsize] * n # Initialize current row with maximum possible value
for j in range(n):
for k in range(n):
curr_row[j] = min(curr_row[j], prev_row[k] + moveCost[grid[i - 1][k]][j] + grid[i][j])
prev_row = curr_row
return min(prev_row)
Java:
import java.util.Arrays;
class Solution {
public int minPathCost(int[][] grid, int[][] moveCost) {
int m = grid.length;
int n = grid[0].length;
int[] prevRow = grid[0];
for (int i = 1; i < m; i++) {
int[] currRow = new int[n];
Arrays.fill(currRow, Integer.MAX_VALUE);
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
currRow[j] = Math.min(currRow[j], prevRow[k] + moveCost[grid[i - 1][k]][j] + grid[i][j]);
}
}
prevRow = currRow;
}
int minCost = Integer.MAX_VALUE;
for (int cost : prevRow) {
minCost = Math.min(minCost, cost);
}
return minCost;
}
}C++:
#include <vector>
#include <limits> // for numeric_limits
class Solution {
public:
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
int m = grid.size();
int n = grid[0].size();
vector<int> prevRow = grid[0];
for (int i = 1; i < m; i++) {
vector<int> currRow(n, numeric_limits<int>::max());
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
currRow[j] = min(currRow[j], prevRow[k] + moveCost[grid[i - 1][k]][j] + grid[i][j]);
}
}
prevRow = currRow;
}
int minCost = numeric_limits<int>::max();
for (int cost : prevRow) {
minCost = min(minCost, cost);
}
return minCost;
}
};These solutions demonstrate the optimized dynamic programming approach, offering a clear and efficient way to solve the "Minimum Path Cost in a Grid" problem. Remember to handle potential integer overflow issues depending on the input constraints.