- {x}
- Subtract the Product and Sum of Digits of an Integer
- Group the People Given the Group Size They Belong To
- Find the Smallest Divisor Given a Threshold
- Minimum Number of Flips to Convert Binary Matrix to Zero Matrix
- Find the Start and End Number of Continuous Ranges
- Iterator for Combination
- Element Appearing More Than 25% In Sorted Array
- Remove Covered Intervals
- Minimum Falling Path Sum II
- Convert Binary Number in a Linked List to Integer
- Sequential Digits
- Maximum Side Length of a Square with Sum Less than or Equal to Threshold
- Shortest Path in a Grid with Obstacles Elimination
- Weather Type in Each Country
- Find Numbers with Even Number of Digits
- Divide Array in Sets of K Consecutive Numbers
- Maximum Number of Occurrences of a Substring
- Read More...

Minimum Falling Path Sum II
Given an n x n integer matrix grid, return the minimum sum of a falling path with non-zero shifts.
A falling path with non-zero shifts is a choice of exactly one element from each row of grid such that no two elements chosen in adjacent rows are in the same column.
Example 1:
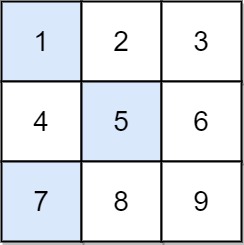
Input: grid = [[1,2,3],[4,5,6],[7,8,9]] Output: 13 Explanation: The possible falling paths are: [1,5,9], [1,5,7], [1,6,7], [1,6,8], [2,4,8], [2,4,9], [2,6,7], [2,6,8], [3,4,8], [3,4,9], [3,5,7], [3,5,9] The falling path with the smallest sum is [1,5,7], so the answer is 13.
Example 2:
Input: grid = [[7]] Output: 7
Constraints:
n == grid.length == grid[i].length1 <= n <= 200-99 <= grid[i][j] <= 99
Minimum Falling Path Sum II
This problem asks for the minimum sum of a falling path in a square grid where no two adjacent elements in the path are in the same column. We can solve this using dynamic programming.
Approach 1: Dynamic Programming with 2D array
This approach uses a 2D array f to store the minimum falling path sum up to each cell. f[i][j] represents the minimum sum ending at cell (i, j).
Algorithm:
-
Initialization: Create a 2D array
fof size (n+1) x n, wherenis the size of the grid. Initialize the first row offto 0. -
Iteration: Iterate through the grid row by row. For each cell
(i, j):- Find the minimum falling path sum among all cells in the previous row (
i-1) excluding the columnj. This is done by iterating through the previous row and taking the minimum value, excluding the cell in the same column. - Update
f[i][j]to be the current cell's value plus the minimum sum found in step 2.
- Find the minimum falling path sum among all cells in the previous row (
-
Result: After iterating through all cells, the minimum falling path sum will be the minimum value in the last row of
f.
Time Complexity: O(n^2), where n is the size of the grid. The nested loops iterate through each cell once.
Space Complexity: O(n^2) due to the 2D array f.
Approach 2: Optimized Dynamic Programming
This approach improves space complexity by using only a few variables to track the minimum and second minimum values from the previous row. This avoids the need for a large 2D array.
Algorithm:
-
Initialization: Initialize
fandg(minimum and second minimum sums from the previous row), andfp(column index off) to 0 and -1 respectively. -
Iteration: Iterate through the grid row by row. For each row:
- Initialize
ffandgg(minimum and second minimum sums for the current row), andffp(column index offf) to infinity and -1 respectively. - Iterate through each cell in the row. Calculate the sum
sby adding the current cell's value to eitherforg(depending on whether the current column is the same asfp). - Update
ff,gg, andffpto maintain the minimum and second minimum sums for the current row.
- Initialize
-
Result: After iterating through all rows,
fwill contain the minimum falling path sum.
Time Complexity: O(n^2), same as Approach 1.
Space Complexity: O(1). This approach only uses a constant number of variables, regardless of the input size.
Code Examples (Python and Java)
Approach 1 (Python):
class Solution:
def minFallingPathSum(self, grid: List[List[int]]) -> int:
n = len(grid)
f = [[0] * n for _ in range(n + 1)]
for i, row in enumerate(grid, 1):
for j, v in enumerate(row):
x = min((f[i - 1][k] for k in range(n) if k != j), default=0)
f[i][j] = v + x
return min(f[n])
Approach 2 (Java):
class Solution {
public int minFallingPathSum(int[][] grid) {
int f = 0, g = 0;
int fp = -1;
final int inf = 1 << 30; // Representing infinity
for (int[] row : grid) {
int ff = inf, gg = inf;
int ffp = -1;
for (int j = 0; j < row.length; ++j) {
int s = (j != fp ? f : g) + row[j];
if (s < ff) {
gg = ff;
ff = s;
ffp = j;
} else if (s < gg) {
gg = s;
}
}
f = ff;
g = gg;
fp = ffp;
}
return f;
}
}The other languages (C++, Go) would have similar implementations, following the same algorithmic approach. Approach 2 is generally preferred due to its better space complexity.