- {x}
- 3Sum With Multiplicity
- Minimize Malware Spread
- Long Pressed Name
- Flip String to Monotone Increasing
- Three Equal Parts
- Minimize Malware Spread II
- Unique Email Addresses
- Binary Subarrays With Sum
- Minimum Falling Path Sum
- Beautiful Array
- Number of Recent Calls
- Shortest Bridge
- Knight Dialer
- Stamping The Sequence
- Reorder Data in Log Files
- Range Sum of BST
- Minimum Area Rectangle
- Read More...

Minimum Falling Path Sum
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
Example 1:
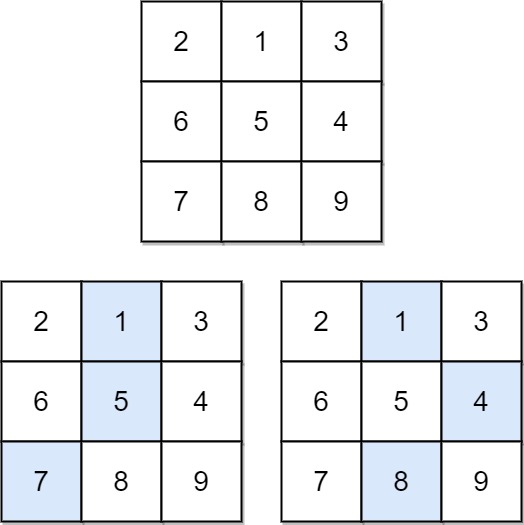
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]] Output: 13 Explanation: There are two falling paths with a minimum sum as shown.
Example 2:
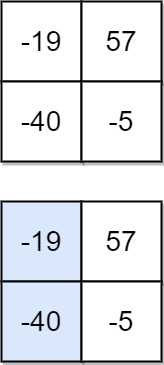
Input: matrix = [[-19,57],[-40,-5]] Output: -59 Explanation: The falling path with a minimum sum is shown.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
Solution Explanation: Minimum Falling Path Sum
This problem asks to find the minimum sum of a falling path through a given square matrix. A falling path starts at any element in the first row and can move to the directly below element or diagonally left/right in the next row.
The most efficient approach is using dynamic programming. We maintain a 1D array f to store the minimum falling path sum ending at each column in the current row. The algorithm iterates through the matrix row by row. For each cell in a row, it considers the minimum falling path sum from the three possible cells above it (directly above, diagonally left, and diagonally right) and adds the current cell's value.
Algorithm:
-
Initialization: Initialize a 1D array
fwith the values of the first row of the matrix. This represents the minimum sum to reach each column in the first row. -
Iteration: Iterate through the remaining rows of the matrix. For each cell
matrix[i][j]:- Create a temporary array
gto store the minimum path sums for the current row. - For each column
j, calculateg[j]by considering the minimum off[j-1],f[j], andf[j+1](handling boundary cases wherej-1orj+1is out of bounds). This represents the minimum path sum reaching the cellmatrix[i][j]from the previous row. - Add
matrix[i][j]tog[j]. - After processing all columns in the current row, copy
gtoffor the next iteration.
- Create a temporary array
-
Result: After processing all rows, the minimum value in
frepresents the minimum falling path sum from the top row to the bottom row.
Time and Space Complexity Analysis:
-
Time Complexity: O(n²), where n is the number of rows (and columns) in the matrix. We iterate through each cell of the matrix once.
-
Space Complexity: O(n). We use a 1D array
fof size n to store the minimum path sums at each column. The temporary arraygalso has size n, so the overall space complexity remains O(n).
Code Explanations (Python3 as example, concepts are similar across other languages):
class Solution:
def minFallingPathSum(self, matrix: List[List[int]]) -> int:
n = len(matrix)
f = [0] * n # Initialize with the first row
for i in range(n):
f[i] = matrix[0][i]
for i in range(1, n): # Iterate from the second row
g = [0] * n # Temporary array for the current row
for j in range(n):
min_above = float('inf') # Initialize with a large value
# Consider the three possible cells above
if j > 0:
min_above = min(min_above, f[j - 1])
min_above = min(min_above, f[j])
if j < n - 1:
min_above = min(min_above, f[j + 1])
g[j] = min_above + matrix[i][j] # update with current cell value
f = g # update f for next row
return min(f) # return the minimum value in f after iterating all rowsThe code follows the algorithm described above. Note the use of float('inf') to initialize min_above to ensure that the minimum is correctly calculated even when j-1 or j+1 are out of bounds. The other language implementations are structurally similar, adapting syntax and standard library functions as needed for each language.