- {x}
- Relative Sort Array
- Lowest Common Ancestor of Deepest Leaves
- Longest Well-Performing Interval
- Smallest Sufficient Team
- Active Businesses
- User Purchase Platform
- Number of Equivalent Domino Pairs
- Shortest Path with Alternating Colors
- Minimum Cost Tree From Leaf Values
- Maximum of Absolute Value Expression
- Reported Posts II
- Largest Unique Number
- Armstrong Number
- Connecting Cities With Minimum Cost
- Parallel Courses
- N-th Tribonacci Number
- Alphabet Board Path
- Read More...

Minimum Cost Tree From Leaf Values
Given an array arr of positive integers, consider all binary trees such that:
- Each node has either
0or2children; - The values of
arrcorrespond to the values of each leaf in an in-order traversal of the tree. - The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.
Among all possible binary trees considered, return the smallest possible sum of the values of each non-leaf node. It is guaranteed this sum fits into a 32-bit integer.
A node is a leaf if and only if it has zero children.
Example 1:
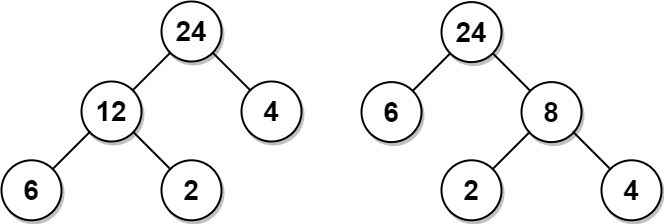
Input: arr = [6,2,4] Output: 32 Explanation: There are two possible trees shown. The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.
Example 2:
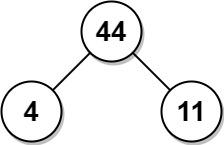
Input: arr = [4,11] Output: 44
Constraints:
2 <= arr.length <= 401 <= arr[i] <= 15- It is guaranteed that the answer fits into a 32-bit signed integer (i.e., it is less than 231).
1130. Minimum Cost Tree From Leaf Values
Problem Description
Given an array arr of positive integers, we need to construct a binary tree where:
- Each node has either 0 or 2 children.
- The values in
arrcorrespond to the leaf nodes in an inorder traversal. - The value of each non-leaf node is the product of the maximum leaf value in its left and right subtrees.
The goal is to find the minimum possible sum of the values of all non-leaf nodes.
Solution Explanation
This problem can be solved efficiently using dynamic programming. The core idea is to build a solution from subproblems. We can define a 2D array dp where dp[i][j] represents the minimum cost to build a subtree from the subarray arr[i:j+1].
We also need a helper array max_arr where max_arr[i][j] stores the maximum value in the subarray arr[i:j+1]. This helps us quickly calculate the product of the maximum values in the left and right subtrees when building a new node.
The dynamic programming recurrence relation is:
dp[i][j] = min(dp[i][k] + dp[k+1][j] + max_arr[i][k] * max_arr[k+1][j]) for k in range(i, j)
This means the minimum cost for the subarray arr[i:j+1] is the minimum cost obtained by splitting the subarray at various points k, recursively solving for the subtrees, and then adding the product of their maximum values.
The base case is when i == j, meaning a single leaf node, in which case the cost is 0.
The final result will be dp[0][n-1], where n is the length of the input array.
Time and Space Complexity
- Time Complexity: O(n^3), due to the three nested loops in the dynamic programming approach.
- Space Complexity: O(n^2), to store the
dpandmax_arrarrays.
Code Implementation (Python)
class Solution:
def mctFromLeafValues(self, arr: List[int]) -> int:
n = len(arr)
dp = [[float('inf')] * n for _ in range(n)]
max_arr = [[0] * n for _ in range(n)]
# Initialize max_arr
for i in range(n):
max_arr[i][i] = arr[i]
for j in range(i + 1, n):
max_arr[i][j] = max(max_arr[i][j - 1], arr[j])
# Base case: single leaf node
for i in range(n):
dp[i][i] = 0
# Fill dp array using dynamic programming
for length in range(2, n + 1):
for i in range(n - length + 1):
j = i + length - 1
for k in range(i, j):
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + max_arr[i][k] * max_arr[k + 1][j])
return dp[0][n - 1]
This Python code efficiently implements the dynamic programming solution described above, providing a clear and concise solution to the problem. Other languages like Java, C++, Go, and TypeScript can be implemented similarly, following the same dynamic programming logic. The core structure and time/space complexity will remain consistent.