{x}
blog image

Minimum Cost to Set Cooking Time

A generic microwave supports cooking times for:

  • at least 1 second.
  • at most 99 minutes and 99 seconds.

To set the cooking time, you push at most four digits. The microwave normalizes what you push as four digits by prepending zeroes. It interprets the first two digits as the minutes and the last two digits as the seconds. It then adds them up as the cooking time. For example,

  • You push 9 5 4 (three digits). It is normalized as 0954 and interpreted as 9 minutes and 54 seconds.
  • You push 0 0 0 8 (four digits). It is interpreted as 0 minutes and 8 seconds.
  • You push 8 0 9 0. It is interpreted as 80 minutes and 90 seconds.
  • You push 8 1 3 0. It is interpreted as 81 minutes and 30 seconds.

You are given integers startAt, moveCost, pushCost, and targetSeconds. Initially, your finger is on the digit startAt. Moving the finger above any specific digit costs moveCost units of fatigue. Pushing the digit below the finger once costs pushCost units of fatigue.

There can be multiple ways to set the microwave to cook for targetSeconds seconds but you are interested in the way with the minimum cost.

Return the minimum cost to set targetSeconds seconds of cooking time.

Remember that one minute consists of 60 seconds.

 

Example 1:

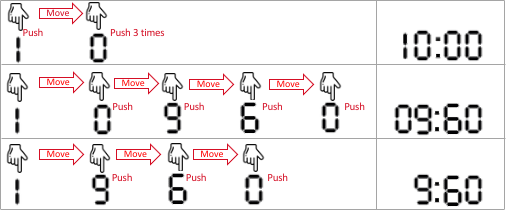
Input: startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
Output: 6
Explanation: The following are the possible ways to set the cooking time.
- 1 0 0 0, interpreted as 10 minutes and 0 seconds.
  The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).
  The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.
- 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.
  The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
  The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.
- 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.
  The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
  The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.

Example 2:

Input: startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
Output: 6
Explanation: The optimal way is to push two digits: 7 6, interpreted as 76 seconds.
The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2). The total cost is: 1 + 2 + 1 + 2 = 6
Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.

 

Constraints:

  • 0 <= startAt <= 9
  • 1 <= moveCost, pushCost <= 105
  • 1 <= targetSeconds <= 6039

Minimum Cost to Set Cooking Time

This problem involves finding the minimum cost to set a cooking time on a microwave given constraints on digit pushing and movement. The solution involves exploring different ways to represent the target time in minutes and seconds and calculating the cost for each representation.

Approach

The core idea is to enumerate all possible ways to represent the targetSeconds as a combination of minutes and seconds, then calculate the cost for each representation. Since the input targetSeconds is at most 6039 (99 minutes and 99 seconds), the number of possible representations is relatively small, making a brute-force approach feasible.

For each representation (minutes and seconds), we convert it into a four-digit string (prepending zeros if necessary). Then, we traverse this string, calculating the cost based on:

  • moveCost: The cost to move the finger to a different digit.
  • pushCost: The cost to push a digit.

We keep track of the minimum cost found among all representations.

Time and Space Complexity

  • Time Complexity: O(1). Although we iterate through possible minute/second combinations, the number of combinations is bounded by a small constant (at most 200 combinations, as minutes can be at most 99, and seconds can be at most 99 + 60 = 159 which means at most 100 * 159). The iteration and cost calculation within each combination takes constant time.

  • Space Complexity: O(1). The algorithm uses a constant amount of extra space regardless of the input size.

Code Explanation (Python)

class Solution:
    def minCostSetTime(
        self, startAt: int, moveCost: int, pushCost: int, targetSeconds: int
    ) -> int:
        def calculate_cost(digits, startAt, moveCost, pushCost):
            cost = 0
            current_digit = startAt
            for digit in digits:
                if int(digit) != current_digit:
                    cost += moveCost
                    current_digit = int(digit)
                cost += pushCost
            return cost
 
        min_cost = float('inf')
        minutes, seconds = divmod(targetSeconds, 60)
 
        # Try different representations: (minutes, seconds) and (minutes-1, seconds+60)
        for minutes, seconds in [(minutes, seconds), (minutes - 1, seconds + 60)]:
            if 0 <= minutes < 100 and 0 <= seconds < 100:
                time_str = "{:02d}{:02d}".format(minutes, seconds)
                cost = calculate_cost(time_str, startAt, moveCost, pushCost)
                min_cost = min(min_cost, cost)
 
        return min_cost

The calculate_cost function efficiently computes the cost for a given four-digit representation. The main part of the code iterates through at most two possible representations ( minutes and seconds or minutes-1 and seconds+60), calculates the cost using calculate_cost, and updates min_cost accordingly.

The other languages (Java, C++, Go) follow a very similar logic and structure, with minor syntactic differences. They all have the same time and space complexity.