- {x}
- Longest Uncommon Subsequence II
- Continuous Subarray Sum
- Longest Word in Dictionary through Deleting
- Contiguous Array
- Beautiful Arrangement
- Word Abbreviation
- Random Pick with Weight
- Minesweeper
- Minimum Absolute Difference in BST
- Lonely Pixel I
- K-diff Pairs in an Array
- Lonely Pixel II
- Game Play Analysis III
- Encode and Decode TinyURL
- Construct Binary Tree from String
- Complex Number Multiplication
- Convert BST to Greater Tree
- Read More...

Minimum Absolute Difference in BST
Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.
Example 1:
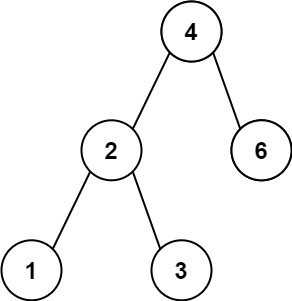
Input: root = [4,2,6,1,3] Output: 1
Example 2:
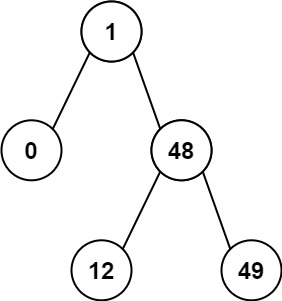
Input: root = [1,0,48,null,null,12,49] Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 104]. 0 <= Node.val <= 105
Note: This question is the same as 783: https://leetcode.com/problems/minimum-distance-between-bst-nodes/
Solution Explanation: Minimum Absolute Difference in BST
This problem asks for the minimum absolute difference between any two nodes in a Binary Search Tree (BST). The key insight is leveraging the inherent property of a BST: an inorder traversal yields a sorted sequence of node values. Therefore, the minimum difference will always exist between two adjacent nodes in this sorted sequence.
Approach: Inorder Traversal
The solution employs an inorder traversal of the BST. Inorder traversal visits nodes in the order: left subtree, root, right subtree. Because it's a BST, this order guarantees the visited nodes are in ascending order. We track the previously visited node's value (pre) and calculate the absolute difference between the current node's value and pre. The minimum of these differences is the final answer.
Algorithm:
-
Initialization:
pre: Stores the value of the previously visited node. Initialized to negative infinity (-inf) to handle the first node.ans: Stores the minimum absolute difference found so far. Initialized to positive infinity (inf).
-
Recursive Inorder Traversal (
dfsfunction):- Base Case: If the current node is
null, return. - Recursive Step (Left Subtree): Recursively traverse the left subtree.
- Current Node Processing:
- Update
answith the minimum ofansand the absolute difference between the current node's value andpre. - Update
preto the current node's value.
- Update
- Recursive Step (Right Subtree): Recursively traverse the right subtree.
- Base Case: If the current node is
-
Return
ans: After the traversal completes,ansholds the minimum absolute difference.
Time and Space Complexity Analysis:
-
Time Complexity: O(N), where N is the number of nodes in the BST. This is because we perform a single inorder traversal, visiting each node exactly once.
-
Space Complexity: O(H), where H is the height of the BST. This is due to the recursive call stack used during the inorder traversal. In the worst case (a skewed BST), H could be N, resulting in O(N) space complexity. In the best case (a balanced BST), H is log₂(N), resulting in O(log N) space complexity.
Code Examples (Python and Java):
Python:
class Solution:
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
pre = float('-inf')
ans = float('inf')
def dfs(node):
nonlocal pre, ans
if not node:
return
dfs(node.left)
ans = min(ans, node.val - pre)
pre = node.val
dfs(node.right)
dfs(root)
return ansJava:
class Solution {
private int pre = Integer.MIN_VALUE;
private int ans = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
dfs(root);
return ans;
}
private void dfs(TreeNode node) {
if (node == null) return;
dfs(node.left);
ans = Math.min(ans, node.val - pre);
pre = node.val;
dfs(node.right);
}
}The code in other languages (C++, Go, TypeScript, Rust, JavaScript) follows a similar structure, adapting the syntax and data types to the respective languages. The core algorithm remains consistent across all implementations.