- {x}
- Airplane Seat Assignment Probability
- Missing Number In Arithmetic Progression
- Meeting Scheduler
- Toss Strange Coins
- Divide Chocolate
- Check If It Is a Straight Line
- Remove Sub-Folders from the Filesystem
- Replace the Substring for Balanced String
- Maximum Profit in Job Scheduling
- Web Crawler
- Find Positive Integer Solution for a Given Equation
- Circular Permutation in Binary Representation
- Maximum Length of a Concatenated String with Unique Characters
- Tiling a Rectangle with the Fewest Squares
- Number of Comments per Post
- Web Crawler Multithreaded
- Array Transformation
- Read More...

Maximum Profit in Job Scheduling
We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].
You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.
If you choose a job that ends at time X you will be able to start another job that starts at time X.
Example 1:
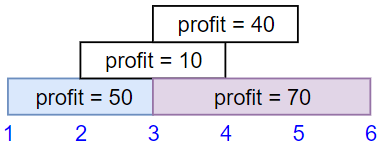
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70] Output: 120 Explanation: The subset chosen is the first and fourth job. Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.
Example 2:
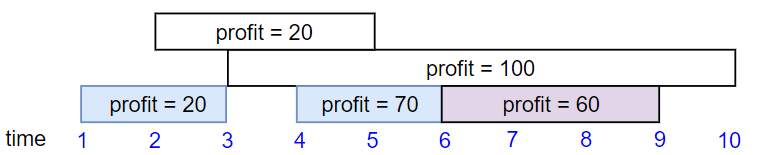
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60] Output: 150 Explanation: The subset chosen is the first, fourth and fifth job. Profit obtained 150 = 20 + 70 + 60.
Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4] Output: 6
Constraints:
1 <= startTime.length == endTime.length == profit.length <= 5 * 1041 <= startTime[i] < endTime[i] <= 1091 <= profit[i] <= 104
1235. Maximum Profit in Job Scheduling
This problem asks to find the maximum profit achievable by scheduling jobs without overlapping time ranges. We are given three arrays: startTime, endTime, and profit, each representing the start time, end time, and profit of a job, respectively.
Approach: Dynamic Programming with Binary Search
The most efficient approach uses dynamic programming combined with binary search for optimal performance.
-
Data Structure: We'll create a custom data structure (e.g., a struct or class) to represent each job, combining
startTime,endTime, andprofit. This will help in sorting and managing jobs easily. -
Sorting: Sort the jobs by their end times in ascending order. This is crucial for efficient dynamic programming.
-
Dynamic Programming: Create a
dparray wheredp[i]represents the maximum profit achievable considering jobs up to indexi. We initializedp[0] = 0. -
Iteration and Binary Search: Iterate through the sorted jobs. For each job
i:- Calculate the maximum profit achievable without including job
i: This is simplydp[i]. - Find the latest non-overlapping job
jusing binary search on the sorted jobs based on their start times. Binary search is efficient for finding the latest non-overlapping job. This works because the jobs are sorted by their end times. - Calculate the maximum profit achievable with including job
i: This isdp[j] + profit[i]. - Update
dp[i+1]as the maximum of these two values.
- Calculate the maximum profit achievable without including job
-
Result: The final element
dp[n](wherenis the number of jobs) will contain the maximum profit.
Time and Space Complexity
- Time Complexity: O(N log N), dominated by the sorting step and the N binary search operations (each taking log N time).
- Space Complexity: O(N) for the
dparray and the job data structure.
Code Implementation (Python)
import bisect
def jobScheduling(startTime, endTime, profit):
jobs = sorted(zip(endTime, startTime, profit)) # Sort by endTime
n = len(profit)
dp = [0] * (n + 1) # Initialize DP array
for i, (et, st, p) in enumerate(jobs):
j = bisect.bisect_right([job[0] for job in jobs], st) # Binary search for latest non-overlapping job
dp[i + 1] = max(dp[i], dp[j] + p) # Update DP array
return dp[n]
Code Implementation (Java)
import java.util.Arrays;
import java.util.Comparator;
class Solution {
public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
int n = profit.length;
int[][] jobs = new int[n][3];
for (int i = 0; i < n; i++) {
jobs[i] = new int[]{endTime[i], startTime[i], profit[i]}; // Store as (endTime, startTime, profit)
}
Arrays.sort(jobs, Comparator.comparingInt(a -> a[0])); // Sort by endTime
int[] dp = new int[n + 1];
for (int i = 0; i < n; i++) {
int j = binarySearch(jobs, i, jobs[i][1]); // Binary search for latest non-overlapping job
dp[i + 1] = Math.max(dp[i], dp[j] + jobs[i][2]); //Update dp array
}
return dp[n];
}
private int binarySearch(int[][] jobs, int right, int target) {
int left = 0;
while (left < right) {
int mid = (left + right) / 2;
if (jobs[mid][1] > target) { // Check if the job does not overlap
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}The Java and Python solutions demonstrate the core dynamic programming and binary search logic. Other languages (C++, JavaScript, etc.) would follow a similar structure, adapting the syntax as needed. Remember to handle edge cases appropriately (e.g., empty input arrays).