{x}
blog image

Maximum Good People Based on Statements

There are two types of persons:

  • The good person: The person who always tells the truth.
  • The bad person: The person who might tell the truth and might lie.

You are given a 0-indexed 2D integer array statements of size n x n that represents the statements made by n people about each other. More specifically, statements[i][j] could be one of the following:

  • 0 which represents a statement made by person i that person j is a bad person.
  • 1 which represents a statement made by person i that person j is a good person.
  • 2 represents that no statement is made by person i about person j.

Additionally, no person ever makes a statement about themselves. Formally, we have that statements[i][i] = 2 for all 0 <= i < n.

Return the maximum number of people who can be good based on the statements made by the n people.

 

Example 1:

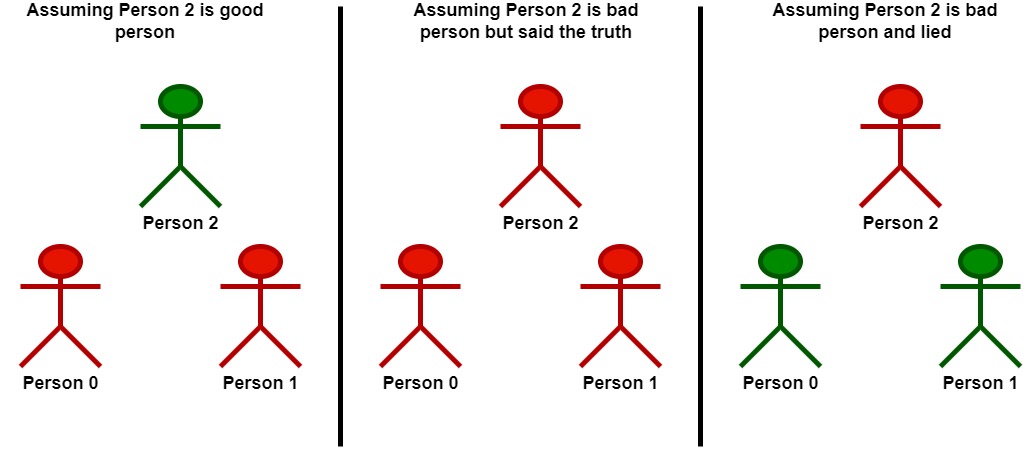
Input: statements = [[2,1,2],[1,2,2],[2,0,2]]
Output: 2
Explanation: Each person makes a single statement.
- Person 0 states that person 1 is good.
- Person 1 states that person 0 is good.
- Person 2 states that person 1 is bad.
Let's take person 2 as the key.
- Assuming that person 2 is a good person:
    - Based on the statement made by person 2, person 1 is a bad person.
    - Now we know for sure that person 1 is bad and person 2 is good.
    - Based on the statement made by person 1, and since person 1 is bad, they could be:
        - telling the truth. There will be a contradiction in this case and this assumption is invalid.
        - lying. In this case, person 0 is also a bad person and lied in their statement.
    - Following that person 2 is a good person, there will be only one good person in the group.
- Assuming that person 2 is a bad person:
    - Based on the statement made by person 2, and since person 2 is bad, they could be:
        - telling the truth. Following this scenario, person 0 and 1 are both bad as explained before.
            - Following that person 2 is bad but told the truth, there will be no good persons in the group.
        - lying. In this case person 1 is a good person.
            - Since person 1 is a good person, person 0 is also a good person.
            - Following that person 2 is bad and lied, there will be two good persons in the group.
We can see that at most 2 persons are good in the best case, so we return 2.
Note that there is more than one way to arrive at this conclusion.

Example 2:

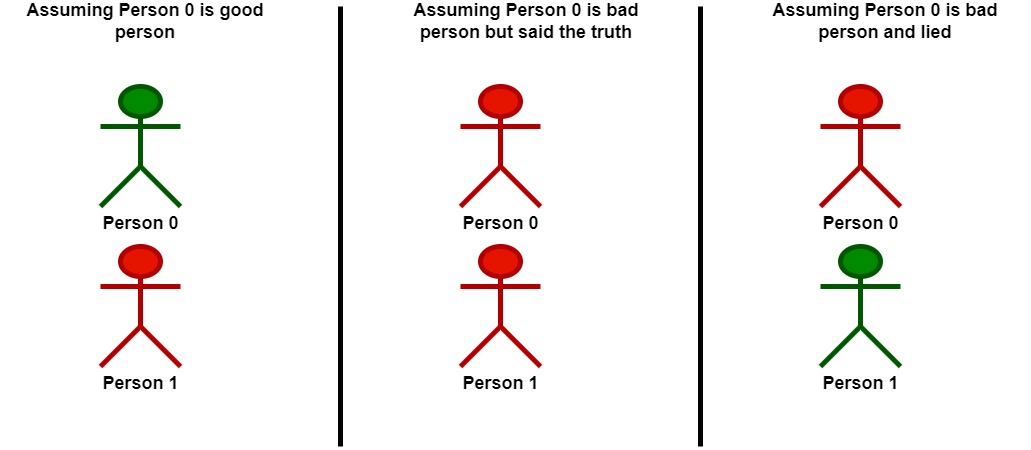
Input: statements = [[2,0],[0,2]]
Output: 1
Explanation: Each person makes a single statement.
- Person 0 states that person 1 is bad.
- Person 1 states that person 0 is bad.
Let's take person 0 as the key.
- Assuming that person 0 is a good person:
    - Based on the statement made by person 0, person 1 is a bad person and was lying.
    - Following that person 0 is a good person, there will be only one good person in the group.
- Assuming that person 0 is a bad person:
    - Based on the statement made by person 0, and since person 0 is bad, they could be:
        - telling the truth. Following this scenario, person 0 and 1 are both bad.
            - Following that person 0 is bad but told the truth, there will be no good persons in the group.
        - lying. In this case person 1 is a good person.
            - Following that person 0 is bad and lied, there will be only one good person in the group.
We can see that at most, one person is good in the best case, so we return 1.
Note that there is more than one way to arrive at this conclusion.

 

Constraints:

  • n == statements.length == statements[i].length
  • 2 <= n <= 15
  • statements[i][j] is either 0, 1, or 2.
  • statements[i][i] == 2

Solution Explanation:

This problem asks to find the maximum number of people who can be considered "good" based on a set of statements they make about each other. A "good" person always tells the truth, while a "bad" person can lie or tell the truth. The statements are represented in a 2D array where statements[i][j] indicates person i's statement about person j (0 for bad, 1 for good, 2 for no statement).

The most efficient approach uses bit manipulation and enumeration. We iterate through all possible combinations of people being "good" (represented by a bitmask). For each combination, we check for consistency: if a person is marked as "good", all their statements must be true. If a statement is inconsistent, we disregard that combination. The solution keeps track of the maximum number of "good" people found in a consistent combination.

Algorithm:

  1. Bitmask Representation: Each integer from 1 to 2n-1 (where n is the number of people) represents a combination of good people. The i-th bit being set indicates that person i is considered "good".

  2. Consistency Check (check function): For each bitmask:

    • Initialize a cnt to count the number of good people in this combination.
    • Iterate through each person i:
      • If the i-th bit is set (person i is "good"):
        • Iterate through person i's statements (statements[i]):
          • If a statement is made (statements[i][j] < 2):
            • Check if the statement is consistent with the current bitmask. If statements[i][j] is 0 (person j is bad) and the j-th bit is set (person j is good), or statements[i][j] is 1 (person j is good) and the j-th bit is not set (person j is bad), then the combination is inconsistent, return 0.
        • If all statements are consistent for person i, increment cnt.

  3. Maximum Count: The check function returns the number of good people for a consistent combination. The main part of the code iterates through all bitmasks, calls check for each, and keeps track of the maximum count found.

Time and Space Complexity:

  • Time Complexity: O(n * 2n). We iterate through all possible combinations of good people (2n combinations), and for each combination, we perform a check that takes O(n) time in the worst case.

  • Space Complexity: O(1). The algorithm uses a constant amount of extra space regardless of the input size.

Code Explanation (Python):

The Python code directly implements this algorithm:

class Solution:
    def maximumGood(self, statements: List[List[int]]) -> int:
        def check(mask: int) -> int:
            cnt = 0
            for i, row in enumerate(statements):
                if mask >> i & 1:  # Check if i-th bit is set (person i is good)
                    for j, x in enumerate(row):
                        if x < 2 and (mask >> j & 1) != x: # Check for inconsistencies
                            return 0
                    cnt += 1
            return cnt
 
        return max(check(i) for i in range(1, 1 << len(statements))) # Iterate through all bitmasks

The other languages (Java, C++, Go, TypeScript) follow the same logic, differing only in syntax and data structures. The core idea of using bit manipulation to efficiently explore all combinations remains the same across all implementations.