{x}
blog image

Maximum Fruits Harvested After at Most K Steps

Fruits are available at some positions on an infinite x-axis. You are given a 2D integer array fruits where fruits[i] = [positioni, amounti] depicts amounti fruits at the position positioni. fruits is already sorted by positioni in ascending order, and each positioni is unique.

You are also given an integer startPos and an integer k. Initially, you are at the position startPos. From any position, you can either walk to the left or right. It takes one step to move one unit on the x-axis, and you can walk at most k steps in total. For every position you reach, you harvest all the fruits at that position, and the fruits will disappear from that position.

Return the maximum total number of fruits you can harvest.

 

Example 1:

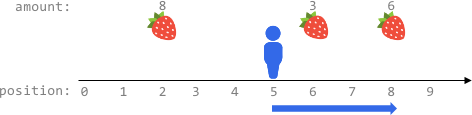
Input: fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
Output: 9
Explanation: 
The optimal way is to:
- Move right to position 6 and harvest 3 fruits
- Move right to position 8 and harvest 6 fruits
You moved 3 steps and harvested 3 + 6 = 9 fruits in total.

Example 2:

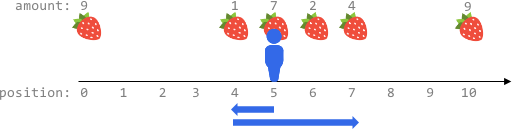
Input: fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
Output: 14
Explanation: 
You can move at most k = 4 steps, so you cannot reach position 0 nor 10.
The optimal way is to:
- Harvest the 7 fruits at the starting position 5
- Move left to position 4 and harvest 1 fruit
- Move right to position 6 and harvest 2 fruits
- Move right to position 7 and harvest 4 fruits
You moved 1 + 3 = 4 steps and harvested 7 + 1 + 2 + 4 = 14 fruits in total.

Example 3:

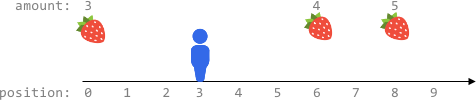
Input: fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
Output: 0
Explanation:
You can move at most k = 2 steps and cannot reach any position with fruits.

 

Constraints:

  • 1 <= fruits.length <= 105
  • fruits[i].length == 2
  • 0 <= startPos, positioni <= 2 * 105
  • positioni-1 < positioni for any i > 0 (0-indexed)
  • 1 <= amounti <= 104
  • 0 <= k <= 2 * 105

Solution Explanation:

This problem asks to find the maximum number of fruits that can be harvested within at most k steps from a starting position startPos. The fruits are represented as a sorted array of [position, amount] pairs.

The optimal solution utilizes a sliding window approach enhanced with a clever optimization to avoid redundant calculations. Instead of brute-forcing all possible combinations of fruit picking, it efficiently tracks the accumulated fruits within a moving window. The window's boundaries are adjusted based on the step constraints.

Algorithm:

  1. Initialization:

    • ans: Stores the maximum number of harvested fruits (initialized to 0).
    • s: Stores the current sum of fruits within the sliding window (initialized to 0).
    • i: Represents the left boundary of the sliding window (initialized to 0).

  2. Iterating through fruits:

    • The outer loop iterates through each fruit (j) in the fruits array.
    • Add the current fruit's amount (fj) to the current sum s.

  3. Sliding Window Adjustment:

    • The while loop checks if the current window violates the step constraint (k).
    • It calculates the total steps needed to reach the current fruit (j) from the starting position, considering the possibility of moving left or right. Then it subtracts the steps needed to reach the current fruit (j) from the leftmost fruit (i) in the window.
    • If the total steps exceed k, it means the left boundary (i) of the window needs to be moved to the right to shorten the window. The fruit at index i is removed from the sum s.

  4. Updating the maximum:

    • After adjusting the sliding window, the current sum s represents the maximum fruits that can be harvested within the step constraint, starting from fruit at index i and ending at fruit at index j.
    • ans is updated to the maximum between ans and s.

  5. Return: The function returns ans, which holds the maximum number of fruits harvested.

Time Complexity Analysis:

The outer loop iterates through each fruit once (O(n), where n is the number of fruits). The inner loop (while loop) can potentially iterate up to n times in the worst case. However, the inner loop's iterations are amortized across the entire process. Each fruit is added to s exactly once in the outer loop, and removed at most once in the inner loop. This leads to a time complexity of O(n) on average.

Space Complexity Analysis:

The algorithm uses a constant amount of extra space for variables (ans, s, i, j). Therefore, the space complexity is O(1).

Code Explanation (Python):

The Python code directly implements the algorithm described above. The min(abs(startPos - fruits[i][0]), abs(startPos - pj)) part efficiently calculates the minimum steps needed to reach either the leftmost or current fruit from startPos, representing the optimal path choice. The other languages follow a very similar implementation, just with different syntax.