{x}
blog image

Maximum Building Height

You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.

However, there are city restrictions on the heights of the new buildings:

  • The height of each building must be a non-negative integer.
  • The height of the first building must be 0.
  • The height difference between any two adjacent buildings cannot exceed 1.

Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [idi, maxHeighti] indicates that building idi must have a height less than or equal to maxHeighti.

It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.

Return the maximum possible height of the tallest building.

 

Example 1:

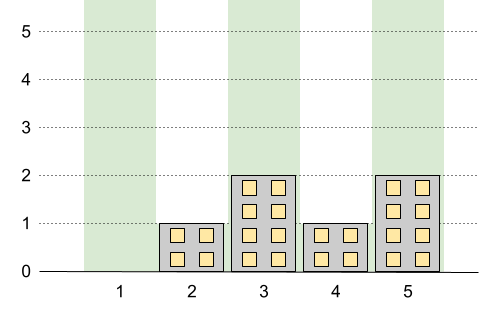
Input: n = 5, restrictions = [[2,1],[4,1]]
Output: 2
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.

Example 2:

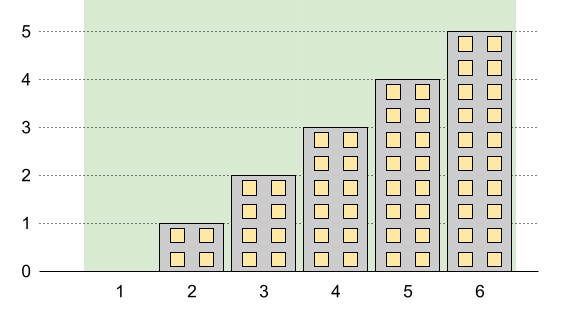
Input: n = 6, restrictions = []
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.

Example 3:

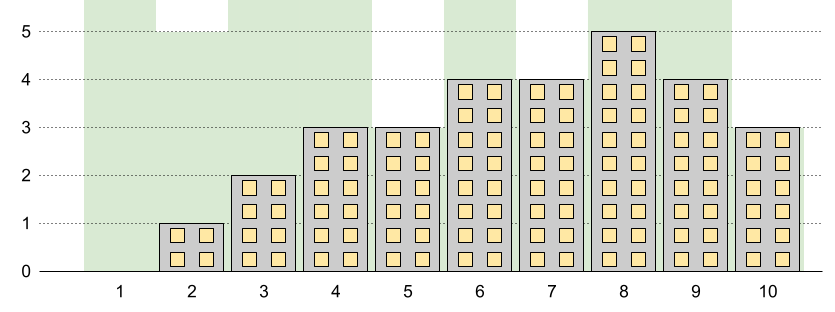
Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.

 

Constraints:

  • 2 <= n <= 109
  • 0 <= restrictions.length <= min(n - 1, 105)
  • 2 <= idi <= n
  • idi is unique.
  • 0 <= maxHeighti <= 109

Solution Explanation: Maximum Building Height

This problem involves finding the maximum possible height of the tallest building, subject to constraints on adjacent building height differences and maximum heights for specific buildings. The optimal solution uses a clever approach combining sorting and mathematical reasoning.

Approach:

  1. Data Preparation:

    • Add two virtual restrictions: [1, 0] (building 1 always has height 0) and [n, n-1] (to handle the last building).
    • Sort the restrictions array by building ID (restrictions[i][0]). This ordering is crucial for efficiently processing constraints.

  2. Forward Pass (Left to Right):

    • Iterate through the sorted restrictions.
    • For each restriction restrictions[i], update its maxHeight (restrictions[i][1]) to be the minimum of its current maxHeight and the maximum height achievable from the previous building. This ensures that the height difference between adjacent buildings never exceeds 1. The formula used is: restrictions[i][1] = min(restrictions[i][1], restrictions[i-1][1] + restrictions[i][0] - restrictions[i-1][0])

  3. Backward Pass (Right to Left):

    • Iterate through the sorted restrictions in reverse order.
    • Similar to the forward pass, update each restriction's maxHeight to consider constraints from the right. The formula is: restrictions[i][1] = min(restrictions[i][1], restrictions[i+1][1] + restrictions[i+1][0] - restrictions[i][0])

  4. Finding the Maximum Height:

    • After both passes, the maxHeight for each restriction represents the maximum achievable height for that building, considering all constraints.
    • The maximum height of the tallest building is not necessarily the maximum of these individual maxHeight values. It could be within a range between two constrained buildings.
    • Iterate through the restrictions, calculating the maximum height possible between each adjacent pair of restrictions using the formula: max_height = max(max_height, (restrictions[i][1] + restrictions[i+1][1] + restrictions[i+1][0] - restrictions[i][0]) // 2) This formula accounts for the constraint that the height must increase and then decrease between the two buildings to achieve the maximum height.

  5. Return Result: The max_height calculated in the final step represents the maximum possible height of the tallest building.

Time and Space Complexity:

  • Time Complexity: O(m log m), where m is the number of restrictions. This is dominated by the sorting step. The forward and backward passes and the final iteration are all linear in m.
  • Space Complexity: O(m), due to the space used to store the sorted restrictions array. In-place modifications could slightly reduce this, but the overall complexity remains linear.

Code Examples (Python):

def maxBuilding(n: int, restrictions: List[List[int]]) -> int:
    r = restrictions + [[1, 0]]  #Add building 1 restriction
    if restrictions[-1][0]!=n:
        r.append([n, n - 1]) #Add last building restriction
 
    r.sort()  #Sort by building ID
    m = len(r)
    
    for i in range(1, m):
        r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0])
    
    for i in range(m - 2, -1, -1):
        r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0])
    
    ans = 0
    for i in range(m - 1):
        ans = max(ans, (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) // 2)
        
    return ans

The code in other languages (Java, C++, Go, TypeScript) follows the same algorithmic structure, only differing in syntax. The core logic of sorting, the forward and backward passes, and the final height calculation remains consistent across all implementations.