{x}
blog image

Kth Smallest Instructions

Bob is standing at cell (0, 0), and he wants to reach destination: (row, column). He can only travel right and down. You are going to help Bob by providing instructions for him to reach destination.

The instructions are represented as a string, where each character is either:

  • 'H', meaning move horizontally (go right), or
  • 'V', meaning move vertically (go down).

Multiple instructions will lead Bob to destination. For example, if destination is (2, 3), both "HHHVV" and "HVHVH" are valid instructions.

However, Bob is very picky. Bob has a lucky number k, and he wants the kth lexicographically smallest instructions that will lead him to destination. k is 1-indexed.

Given an integer array destination and an integer k, return the kth lexicographically smallest instructions that will take Bob to destination.

 

Example 1:

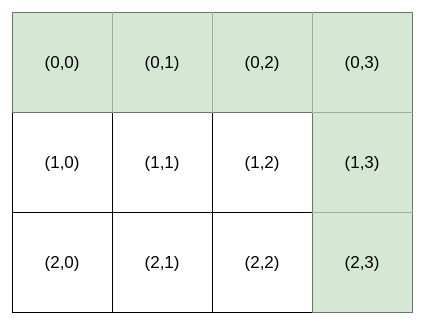
Input: destination = [2,3], k = 1
Output: "HHHVV"
Explanation: All the instructions that reach (2, 3) in lexicographic order are as follows:
["HHHVV", "HHVHV", "HHVVH", "HVHHV", "HVHVH", "HVVHH", "VHHHV", "VHHVH", "VHVHH", "VVHHH"].

Example 2:

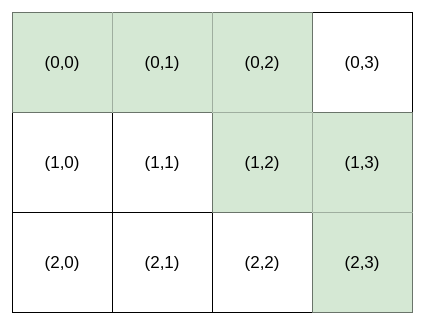
Input: destination = [2,3], k = 2
Output: "HHVHV"

Example 3:

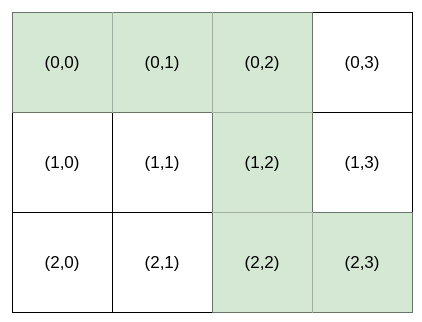
Input: destination = [2,3], k = 3
Output: "HHVVH"

 

Constraints:

  • destination.length == 2
  • 1 <= row, column <= 15
  • 1 <= k <= nCr(row + column, row), where nCr(a, b) denotes a choose b​​​​​.

Solution Explanation

This problem asks to find the k-th lexicographically smallest string representing a path from (0,0) to (row, column) using only 'H' (horizontal move) and 'V' (vertical move).

The solution uses a combinatorial approach. The total number of paths is given by nCr(row + column, row) (or equivalently nCr(row + column, column)), where nCr(n, k) denotes "n choose k". We iterate through the possible moves, deciding at each step whether to move horizontally or vertically based on the remaining number of horizontal and vertical moves and the value of k.

Algorithm:

  1. Precompute Combinations: We first precompute the binomial coefficients (combinations) using dynamic programming. This is done to avoid redundant calculations of nCr within the main loop. The c[i][j] array stores nCr(i, j).

  2. Iterative Path Construction: The core logic lies in the loop that iterates row + column times. In each iteration:

    • If there are no horizontal moves left (h == 0), we must move vertically ('V').
    • Otherwise, we calculate the number of paths that start with 'V' (x = c[v + h - 1][h - 1]).
    • If k is greater than x, it means the k-th lexicographically smallest path starts with 'V'. We append 'V' to the result, decrement v, and subtract x from k (because we've considered all paths starting with 'V').
    • Otherwise, the k-th path starts with 'H'. We append 'H' to the result and decrement h.

  3. Return Result: Finally, we return the constructed string.

Time Complexity Analysis:

  • Precomputation: The precomputation of binomial coefficients takes O((row + column)^2) time due to the nested loops in the DP approach.
  • Path Construction: The loop iterates row + column times. Each iteration takes constant time. Therefore, the path construction takes O(row + column) time.
  • Overall: The dominant factor is the precomputation, so the overall time complexity is O((row + column)^2).

Space Complexity Analysis:

  • Precomputation: We use a 2D array c of size O((row + column)^2) to store binomial coefficients.
  • Path Construction: The space used for the ans string is O(row + column).
  • Overall: The space complexity is dominated by the c array, resulting in O((row + column)^2) space complexity.

Code Explanation (Python):

The Python code uses the comb function from the scipy.special module for efficient binomial coefficient calculation. If scipy is not available, a manual DP-based calculation (as shown in other languages) should be used instead. The rest of the algorithm follows the steps described above.

Code Explanation (Other Languages):

The Java, C++, and Go codes implement the same algorithm but explicitly calculate the binomial coefficients using dynamic programming. They all achieve the same time and space complexity. Note that C++ uses memset for efficient array initialization.

The choice of language affects only the syntax and minor implementation details, but the underlying algorithm and complexity remain consistent across all provided solutions.