{x}
blog image

Island Perimeter

You are given row x col grid representing a map where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.

Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).

The island doesn't have "lakes", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.

 

Example 1:

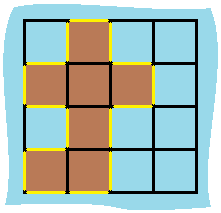
Input: grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
Output: 16
Explanation: The perimeter is the 16 yellow stripes in the image above.

Example 2:

Input: grid = [[1]]
Output: 4

Example 3:

Input: grid = [[1,0]]
Output: 4

 

Constraints:

  • row == grid.length
  • col == grid[i].length
  • 1 <= row, col <= 100
  • grid[i][j] is 0 or 1.
  • There is exactly one island in grid.

Solution Explanation

This problem asks to find the perimeter of an island represented in a grid. The island consists of cells with value 1, and water is represented by 0. The perimeter is calculated by counting the sides of land cells that are not adjacent to another land cell.

The solution iterates through each cell of the grid. For each land cell (grid[i][j] == 1), it initially assumes a perimeter of 4 (all four sides). Then, it checks the adjacent cells (right and down) and subtracts 2 from the perimeter for each adjacent land cell because these sides are shared and should not be counted twice. The final perimeter is the sum of all such calculations for each land cell.

Time Complexity Analysis

The solution iterates through each cell of the grid exactly once. Therefore, the time complexity is O(M*N), where M and N are the dimensions of the grid.

Space Complexity Analysis

The solution uses a constant amount of extra space to store variables like ans, m, n, i, and j. The space complexity is thus O(1), which is constant.

Code Explanation (Python)

class Solution:
    def islandPerimeter(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0]) #Get dimensions of the grid
        ans = 0 #Initialize perimeter
        for i in range(m): #Iterate through rows
            for j in range(n): #Iterate through columns
                if grid[i][j] == 1: #Check if it's a land cell
                    ans += 4 #Assume initial perimeter of 4
                    if i < m - 1 and grid[i + 1][j] == 1: #Check down
                        ans -= 2 #Subtract 2 if adjacent land cell is below
                    if j < n - 1 and grid[i][j + 1] == 1: #Check right
                        ans -= 2 #Subtract 2 if adjacent land cell is to the right
        return ans #Return the calculated perimeter

The other language solutions follow the same logic, adapting the syntax to their respective languages. The core algorithm remains consistent across all implementations.