- {x}
- Flip Columns For Maximum Number of Equal Rows
- Adding Two Negabinary Numbers
- Number of Submatrices That Sum to Target
- Project Employees I
- Project Employees II
- Project Employees III
- Occurrences After Bigram
- Letter Tile Possibilities
- Insufficient Nodes in Root to Leaf Paths
- Smallest Subsequence of Distinct Characters
- Sales Analysis I
- Sales Analysis II
- Sales Analysis III
- Sum of Digits in the Minimum Number
- High Five
- Brace Expansion
- Confusing Number II
- Read More...

Insufficient Nodes in Root to Leaf Paths
Given the root of a binary tree and an integer limit, delete all insufficient nodes in the tree simultaneously, and return the root of the resulting binary tree.
A node is insufficient if every root to leaf path intersecting this node has a sum strictly less than limit.
A leaf is a node with no children.
Example 1:
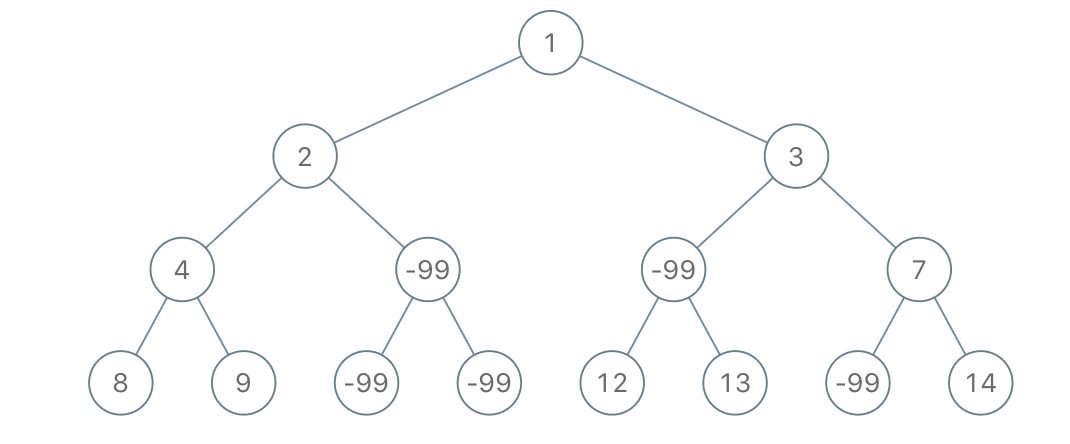
Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1 Output: [1,2,3,4,null,null,7,8,9,null,14]
Example 2:
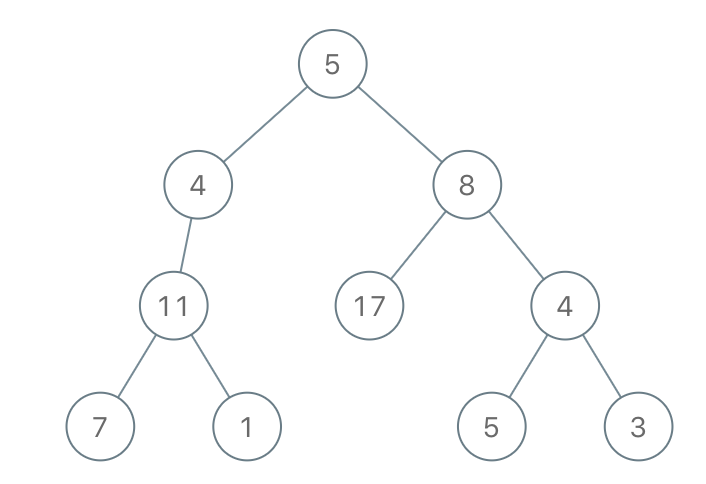
Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22 Output: [5,4,8,11,null,17,4,7,null,null,null,5]
Example 3:
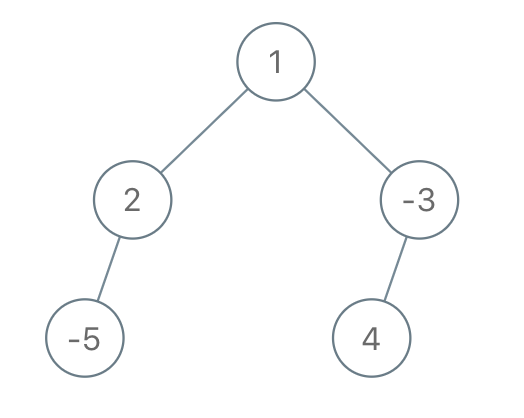
Input: root = [1,2,-3,-5,null,4,null], limit = -1 Output: [1,null,-3,4]
Constraints:
- The number of nodes in the tree is in the range
[1, 5000]. -105 <= Node.val <= 105-109 <= limit <= 109
Solution Explanation:
This problem requires removing nodes from a binary tree where all root-to-leaf paths passing through the node have a sum less than a given limit. The solution uses a post-order Depth-First Search (DFS) traversal to efficiently prune the tree.
Approach:
The key idea is to perform a post-order traversal of the tree. This ensures that we process the children of a node before the node itself. For each node, we recursively check if its children are sufficient (i.e., meet the limit condition). If a child is insufficient, it's removed. After processing the children, we check the current node itself. If both children have been removed, the current node is also removed.
Algorithm:
-
Base Case: If the current node is
null, returnnull. -
Leaf Node Check: If the current node is a leaf node (no children), check if the sum of the path from the root to this leaf node (calculated by subtracting the node's value from the
limit) is less than or equal to 0. If it is, return the node; otherwise, returnnull(remove the leaf node). -
Recursive Calls: Recursively call the
sufficientSubsetfunction on the left and right children of the current node, updating thelimitby subtracting the current node's value. -
Node Removal: After processing the children, if both children are
null(meaning they were removed), returnnull(remove the current node); otherwise, return the current node.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited once during the post-order traversal.
Space Complexity: O(H), where H is the height of the tree. The space complexity is dominated by the recursion stack used for DFS. In the worst case (a skewed tree), H could be equal to N. In the best case (a balanced tree), H is log₂(N).
Code Explanation (Python):
class Solution:
def sufficientSubset(self, root: Optional[TreeNode], limit: int) -> Optional[TreeNode]:
if root is None: #Base case: empty subtree
return None
limit -= root.val #Update limit for the subtree rooted at this node
if root.left is None and root.right is None: #Leaf node check
return None if limit > 0 else root #remove leaf if limit not met
root.left = self.sufficientSubset(root.left, limit) #Recursive call on left child
root.right = self.sufficientSubset(root.right, limit) #Recursive call on right child
return None if root.left is None and root.right is None else root #Remove current node if both children removedThe code in other languages (Java, C++, Go, TypeScript, JavaScript) follows the same algorithm and logic, only differing in syntax. The key components—the base case, leaf node check, recursive calls, and node removal logic—remain consistent across all implementations.