- {x}
- Construct Binary Tree from Preorder and Postorder Traversal
- Find and Replace Pattern
- Sum of Subsequence Widths
- Surface Area of 3D Shapes
- Groups of Special-Equivalent Strings
- All Possible Full Binary Trees
- Maximum Frequency Stack
- Monotonic Array
- Increasing Order Search Tree
- Bitwise ORs of Subarrays
- Orderly Queue
- RLE Iterator
- Online Stock Span
- Numbers At Most N Given Digit Set
- Valid Permutations for DI Sequence
- Fruit Into Baskets
- Sort Array By Parity
- Read More...

Increasing Order Search Tree
Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:
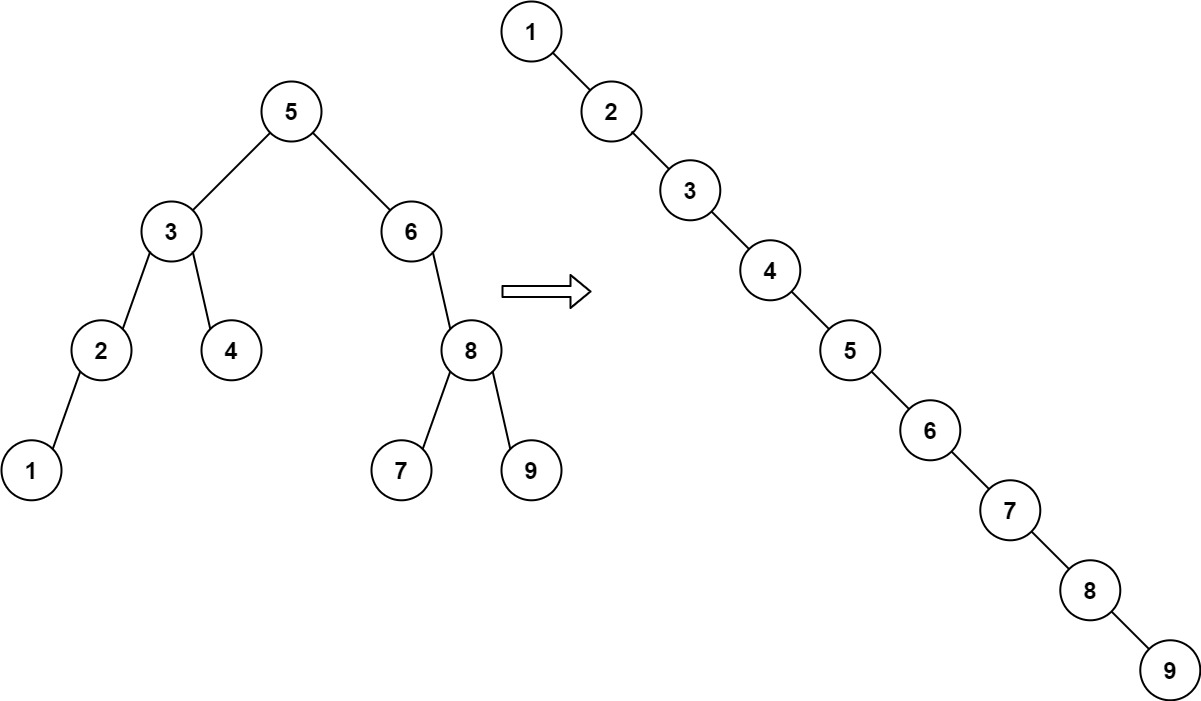
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9] Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
Example 2:
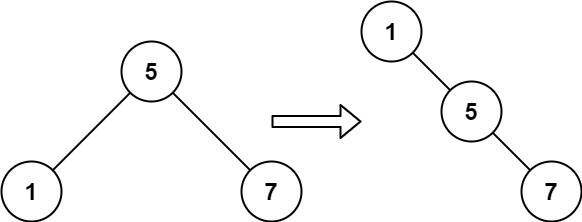
Input: root = [5,1,7] Output: [1,null,5,null,7]
Constraints:
- The number of nodes in the given tree will be in the range
[1, 100]. 0 <= Node.val <= 1000
Solution Explanation: Increasing Order Search Tree
This problem requires transforming a given binary search tree (BST) into a right-skewed singly linked list where each node only has a right child, representing the in-order traversal of the original BST.
Approach:
The most efficient way to solve this problem is through Depth-First Search (DFS) using an in-order traversal. In-order traversal inherently visits nodes in ascending order in a BST. We modify the tree structure during the traversal itself.
We use a dummy node as a starting point for the new linked list. A prev pointer tracks the last node added to the list. The algorithm follows these steps:
-
Initialization: Create a
dummynode withval = 0. Itsrightchild will become the head of our new list. Initializeprevto point todummy. -
DFS In-order Traversal: Recursively traverse the BST using in-order traversal:
- Left Subtree: Recursively process the left subtree.
- Current Node: After processing the left subtree, the
prevpointer points to the last node added to the linked list. We attach the current node to the right ofprev. Then, we set the current node's left child tonullto create the singly-linked structure. Finally, updateprevto point to the current node. - Right Subtree: Recursively process the right subtree.
-
Return: After the traversal, the
dummy.rightnode points to the head of the newly created linked list (the transformed BST).
Time and Space Complexity:
- Time Complexity: O(N), where N is the number of nodes in the BST. We visit each node exactly once during the in-order traversal.
- Space Complexity: O(H) in the average case, and O(N) in the worst case. H is the height of the tree, representing the space used by the recursive call stack during DFS. In a balanced BST, H is log(N), while in a skewed tree, H is N.
Code Implementation (Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def increasingBST(self, root: TreeNode) -> TreeNode:
dummy = TreeNode(0) # Dummy node
prev = dummy # Pointer to the last node added
def inorder(node):
nonlocal prev # Access and modify prev in the inner function
if node:
inorder(node.left)
prev.right = node
node.left = None # Crucial step: remove left child
prev = node
inorder(node.right)
inorder(root)
return dummy.rightThe other languages (Java, C++, Go, TypeScript) follow the same algorithm; only the syntax differs. The core logic remains consistent across all implementations. The key to understanding this solution is grasping how the prev pointer cleverly maintains the structure of the singly-linked list during the in-order traversal, ensuring that the nodes are connected in increasing order.