- {x}
- Minimum Number of Swaps to Make the String Balanced
- Find the Longest Valid Obstacle Course at Each Position
- Employees With Missing Information
- Binary Searchable Numbers in an Unsorted Array
- Number of Strings That Appear as Substrings in Word
- Array With Elements Not Equal to Average of Neighbors
- Minimum Non-Zero Product of the Array Elements
- Last Day Where You Can Still Cross
- Find if Path Exists in Graph
- First and Last Call On the Same Day
- Count Nodes Equal to Sum of Descendants
- Minimum Time to Type Word Using Special Typewriter
- Maximum Matrix Sum
- Number of Ways to Arrive at Destination
- Number of Ways to Separate Numbers
- Employees Whose Manager Left the Company
- Find Greatest Common Divisor of Array
- Read More...

Find if Path Exists in Graph
There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
You want to determine if there is a valid path that exists from vertex source to vertex destination.
Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.
Example 1:
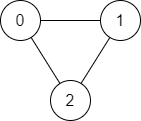
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2 Output: true Explanation: There are two paths from vertex 0 to vertex 2: - 0 → 1 → 2 - 0 → 2
Example 2:
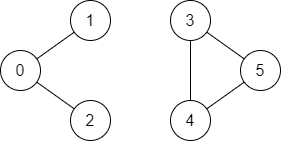
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5 Output: false Explanation: There is no path from vertex 0 to vertex 5.
Constraints:
1 <= n <= 2 * 1050 <= edges.length <= 2 * 105edges[i].length == 20 <= ui, vi <= n - 1ui != vi0 <= source, destination <= n - 1- There are no duplicate edges.
- There are no self edges.
1971. Find if Path Exists in Graph
Description
Given a graph represented as an adjacency list, determine if a path exists between a source and destination node.
Solutions
Three approaches are presented: Depth-First Search (DFS), Breadth-First Search (BFS), and Union-Find.
Solution 1: Depth-First Search (DFS)
This recursive approach explores the graph depth-wise.
Algorithm:
- Build Adjacency List: Convert the input
edgesinto an adjacency listgwhereg[i]contains all neighbors of nodei. - DFS Function:
- Base Case: If the current node
iis thedestination, returntrue. - Mark the current node
ias visited in thevisset. - Recursively call
dfsfor each unvisited neighbor ofi. If any recursive call returnstrue, returntrue. - If no path to the
destinationis found from the current node, returnfalse.
- Base Case: If the current node
- Initial Call: Call
dfs(source)to start the search.
Time Complexity: O(V + E), where V is the number of vertices (nodes) and E is the number of edges. This is because each node and edge is visited at most once.
Space Complexity: O(V + E) in the worst case due to the recursion stack and the adjacency list. In practice, the space usage is often less than this due to tail-call optimization in some languages.
Code (Python):
class Solution:
def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
g = [[] for _ in range(n)]
for u, v in edges:
g[u].append(v)
g[v].append(u)
vis = set()
def dfs(i: int) -> bool:
if i == destination:
return True
vis.add(i)
for j in g[i]:
if j not in vis and dfs(j):
return True
return False
return dfs(source)Code (Java):
class Solution {
private int destination;
private boolean[] vis;
private List<Integer>[] g;
public boolean validPath(int n, int[][] edges, int source, int destination) {
this.destination = destination;
vis = new boolean[n];
g = new ArrayList[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (int[] e : edges) {
int u = e[0], v = e[1];
g[u].add(v);
g[v].add(u);
}
return dfs(source);
}
private boolean dfs(int i) {
if (i == destination) {
return true;
}
vis[i] = true;
for (int j : g[i]) {
if (!vis[j] && dfs(j)) {
return true;
}
}
return false;
}
}Similar code can be written in other languages following the same logic.
Solution 2: Breadth-First Search (BFS)
This iterative approach explores the graph level by level.
Algorithm:
- Build Adjacency List: Same as in DFS.
- BFS:
- Initialize a queue
qwith thesourcenode. - Initialize a
visset to track visited nodes. Addsourcetovis. - While the queue is not empty:
- Dequeue a node
i. - If
iis thedestination, returntrue. - For each unvisited neighbor
jofi:- Add
jtoqandvis.
- Add
- Dequeue a node
- If the queue becomes empty without finding the
destination, returnfalse.
- Initialize a queue
Time Complexity: O(V + E). Similar to DFS, each node and edge is visited at most once.
Space Complexity: O(V) in the worst case because the queue can contain at most all nodes. The vis set also uses O(V) space.
Code (Python):
from collections import deque
class Solution:
def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
g = [[] for _ in range(n)]
for u, v in edges:
g[u].append(v)
g[v].append(u)
q = deque([source])
vis = {source}
while q:
i = q.popleft()
if i == destination:
return True
for j in g[i]:
if j not in vis:
vis.add(j)
q.append(j)
return FalseSolution 3: Union-Find
This approach uses a disjoint-set data structure to efficiently determine connectivity.
Algorithm:
- Initialize Union-Find: Create a
UnionFinddata structure withnnodes. - Merge Edges: Iterate through
edges. For each edge(u, v), merge the sets containinguandvusing theunionoperation of theUnionFindstructure. - Check Connectivity: After merging all edges, check if
sourceanddestinationbelong to the same set using thefindoperation. If they do, there is a path; otherwise, there isn't.
Time Complexity: The time complexity is dominated by the union and find operations. A well-implemented Union-Find structure achieves amortized time complexity of almost O(1) for each operation using path compression and union by rank. Therefore, the overall time complexity is O(E + V), where E is the number of edges, and V is the number of vertices.
Space Complexity: O(V) to store the parent array in the Union-Find data structure.
Code (Python):
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.rank = [0] * n
def find(self, i):
if self.parent[i] == i:
return i
self.parent[i] = self.find(self.parent[i])
return self.parent[i]
def union(self, i, j):
root_i = self.find(i)
root_j = self.find(j)
if root_i != root_j:
if self.rank[root_i] < self.rank[root_j]:
self.parent[root_i] = root_j
elif self.rank[root_i] > self.rank[root_j]:
self.parent[root_j] = root_i
else:
self.parent[root_j] = root_i
self.rank[root_i] += 1
return True
return False
class Solution:
def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
uf = UnionFind(n)
for u, v in edges:
uf.union(u, v)
return uf.find(source) == uf.find(destination)Remember to adapt the Union-Find implementation details for other languages, as the specifics might differ slightly. However, the core algorithm remains the same. The provided Python code shows a path compression and union by rank optimized version for better performance.