- {x}
- Maximum Number of Achievable Transfer Requests
- Find Nearest Right Node in Binary Tree
- Design Parking System
- Alert Using Same Key-Card Three or More Times in a One Hour Period
- Find Valid Matrix Given Row and Column Sums
- Find Servers That Handled Most Number of Requests
- Sellers With No Sales
- Special Array With X Elements Greater Than or Equal X
- Even Odd Tree
- Maximum Number of Visible Points
- Minimum One Bit Operations to Make Integers Zero
- Check If Two Expression Trees are Equivalent
- Find the Missing IDs
- Maximum Nesting Depth of the Parentheses
- Maximal Network Rank
- Split Two Strings to Make Palindrome
- Count Subtrees With Max Distance Between Cities
- Read More...

Even Odd Tree
A binary tree is named Even-Odd if it meets the following conditions:
- The root of the binary tree is at level index
0, its children are at level index1, their children are at level index2, etc. - For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
- For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).
Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.
Example 1:
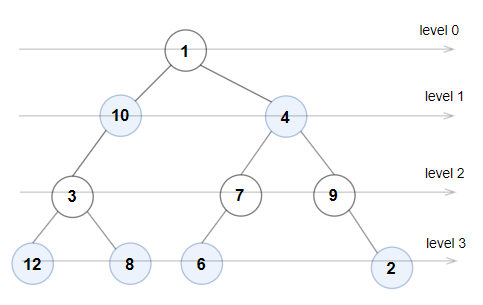
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2] Output: true Explanation: The node values on each level are: Level 0: [1] Level 1: [10,4] Level 2: [3,7,9] Level 3: [12,8,6,2] Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
Example 2:
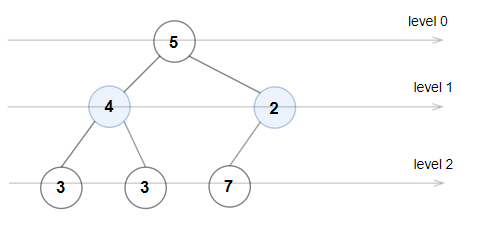
Input: root = [5,4,2,3,3,7] Output: false Explanation: The node values on each level are: Level 0: [5] Level 1: [4,2] Level 2: [3,3,7] Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.
Example 3:
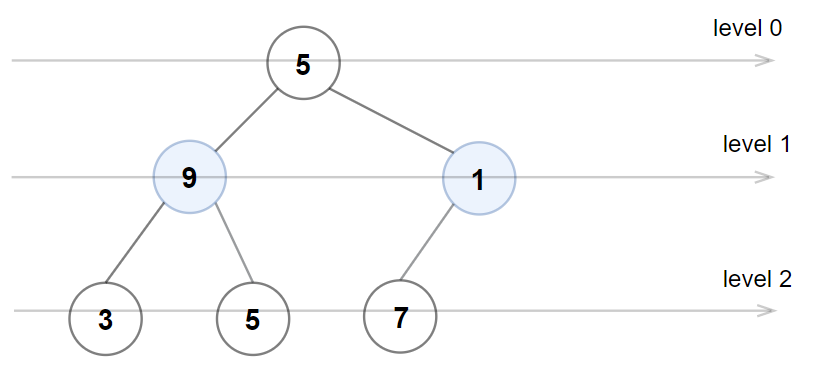
Input: root = [5,9,1,3,5,7] Output: false Explanation: Node values in the level 1 should be even integers.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 106
Solution Explanation for Even Odd Tree
This problem asks us to determine if a binary tree is an "Even-Odd Tree". An Even-Odd Tree satisfies these conditions:
- Level Indexing: The root is at level 0, its children at level 1, and so on.
- Even Levels: Nodes at even levels must have odd values and be strictly increasing from left to right.
- Odd Levels: Nodes at odd levels must have even values and be strictly decreasing from left to right.
Both Breadth-First Search (BFS) and Depth-First Search (DFS) approaches are efficient solutions. Let's examine each:
Solution 1: Breadth-First Search (BFS)
BFS is well-suited for level-order traversal. We process nodes level by level, checking the conditions for each level.
Algorithm:
- Initialization: Use a queue to store nodes for BFS traversal. Initialize
evenflag to track even/odd level. - Level Processing: Iterate while the queue is not empty. Process all nodes at the current level.
- Even Level Check: If
evenis true (even level):- Check if the node's value is even or if it's not strictly increasing compared to the previous node. If either is true, the tree is not Even-Odd.
- Odd Level Check: If
evenis false (odd level):- Check if the node's value is odd or if it's not strictly decreasing compared to the previous node. If either is true, the tree is not Even-Odd.
- Update: After processing a level, toggle the
evenflag and move to the next level.
Time Complexity: O(N), where N is the number of nodes. We visit each node once. Space Complexity: O(W), where W is the maximum width of the tree. In the worst case (a complete binary tree), W can be N, so space complexity is O(N).
Solution 2: Depth-First Search (DFS)
DFS uses recursion to traverse the tree. We maintain the current level and check the conditions recursively.
Algorithm:
- Helper Function (
dfs): A recursive helper function takes the current node and level as input. - Base Case: If the node is null, return
true(it satisfies the condition). - Even/Odd Check: Similar to BFS, check the conditions based on the level's parity.
- Update: If all checks pass, recursively call
dfson the left and right children, updating the level. - Hash Table: A hash table (
din the code) stores the last seen value for each level to efficiently compare with the next node's value within the level.
Time Complexity: O(N). We visit each node once. Space Complexity: O(H), where H is the height of the tree. In the worst-case scenario (a skewed tree), H can be N, leading to O(N) space complexity.
Code Examples (Python):
BFS (Python):
from collections import deque
def isEvenOddTree(root):
q = deque([root])
even = True
while q:
level_size = len(q)
prev = (0 if even else float('inf')) #Initialize prev appropriately for even/odd
for _ in range(level_size):
node = q.popleft()
if even:
if node.val % 2 == 0 or node.val <= prev:
return False
else:
if node.val % 2 != 0 or node.val >= prev:
return False
prev = node.val
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
even = not even
return True
DFS (Python):
def isEvenOddTree(root):
d = {} # Hash table to store last seen value for each level
def dfs(node, level):
if not node:
return True
even = level % 2 == 0
prev = d.get(level, 0 if even else float('inf')) #Handle default for even/odd
if even:
if node.val % 2 == 0 or node.val <= prev:
return False
else:
if node.val % 2 != 0 or node.val >= prev:
return False
d[level] = node.val
return dfs(node.left, level + 1) and dfs(node.right, level + 1)
return dfs(root, 0)
Both solutions are valid and have similar time and space complexities. The choice between BFS and DFS might depend on personal preference or specific constraints of a problem. BFS might be slightly more intuitive for level-order processing, while DFS might be easier to implement recursively.