- {x}
- Get Biggest Three Rhombus Sums in a Grid
- Minimum XOR Sum of Two Arrays
- Check if Word Equals Summation of Two Words
- Maximum Value after Insertion
- Process Tasks Using Servers
- Minimum Skips to Arrive at Meeting On Time
- Egg Drop With 2 Eggs and N Floors
- Count Pairs in Two Arrays
- Determine Whether Matrix Can Be Obtained By Rotation
- Reduction Operations to Make the Array Elements Equal
- Minimum Number of Flips to Make the Binary String Alternating
- Minimum Space Wasted From Packaging
- The Latest Login in 2020
- Cutting Ribbons
- Page Recommendations II
- Check if All the Integers in a Range Are Covered
- Find the Student that Will Replace the Chalk
- Read More...

Determine Whether Matrix Can Be Obtained By Rotation
Given two n x n binary matrices mat and target, return true if it is possible to make mat equal to target by rotating mat in 90-degree increments, or false otherwise.
Example 1:
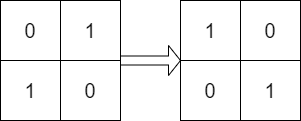
Input: mat = [[0,1],[1,0]], target = [[1,0],[0,1]] Output: true Explanation: We can rotate mat 90 degrees clockwise to make mat equal target.
Example 2:
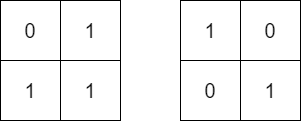
Input: mat = [[0,1],[1,1]], target = [[1,0],[0,1]] Output: false Explanation: It is impossible to make mat equal to target by rotating mat.
Example 3:
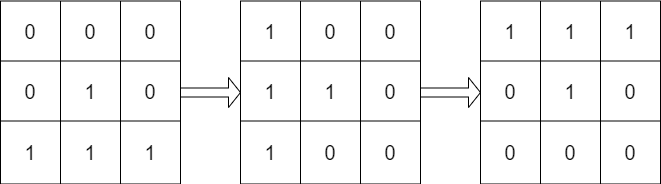
Input: mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]] Output: true Explanation: We can rotate mat 90 degrees clockwise two times to make mat equal target.
Constraints:
n == mat.length == target.lengthn == mat[i].length == target[i].length1 <= n <= 10mat[i][j]andtarget[i][j]are either0or1.
Solution Explanation
This problem asks whether matrix mat can be transformed into matrix target by rotating it 90 degrees clockwise multiple times. The solution involves rotating mat and comparing it to target after each rotation.
Approach:
Both solutions leverage the fact that a 90-degree clockwise rotation can be achieved by transposing the matrix and then reversing each row. Solution 1 implements the rotation in-place, while Solution 2 creates a new rotated matrix in each iteration.
Solution 1 (In-place Rotation):
This solution uses an in-place rotation algorithm. The core of this solution is the rotate function, which efficiently rotates a square matrix by 90 degrees clockwise. It iterates through the matrix using nested loops and swaps elements to achieve the rotation. The equals function compares two matrices for equality. The main part of the code repeatedly calls the rotate function and compares the rotated matrix with the target matrix. If a match is found at any point, the function returns true; otherwise, it returns false after four rotations.
Solution 2 (Creating New Rotated Matrices):
This solution performs rotation by creating a new rotated matrix in each step. Python's concise zip(*mat[::-1]) efficiently transposes and reverses the matrix, resulting in a 90-degree clockwise rotation. The comparison and loop structure remain the same as in Solution 1.
Time Complexity Analysis:
-
Solution 1: The
rotatefunction has a time complexity of O(n²), where n is the dimension of the square matrix. This function is called up to 4 times. Theequalsfunction also has a time complexity of O(n²). Therefore, the overall time complexity of Solution 1 is O(n²). -
Solution 2: The matrix creation and comparison operations in each iteration also have a time complexity of O(n²). Since the loop iterates up to 4 times, the overall time complexity remains O(n²).
Space Complexity Analysis:
-
Solution 1: This solution performs in-place rotation, so the space complexity is O(1), which is constant.
-
Solution 2: This solution creates new rotated matrices in each iteration, leading to a space complexity of O(n²) due to the creation of intermediate matrices.
Code Examples:
The provided code includes solutions in multiple programming languages (Python, Java, C++, Go, TypeScript, and Rust) demonstrating both approaches. The Python solutions are particularly concise due to Python's list manipulation capabilities. Note that the equals functions in Java and Go are necessary because direct comparison of matrices using == does not work correctly in those languages.
In summary, both solutions correctly solve the problem; however, Solution 1 is generally preferred because of its better space complexity. The choice between them might depend on the specific programming language and constraints.