{x}
blog image

Detect Cycles in 2D Grid

Given a 2D array of characters grid of size m x n, you need to find if there exists any cycle consisting of the same value in grid.

A cycle is a path of length 4 or more in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the same value of the current cell.

Also, you cannot move to the cell that you visited in your last move. For example, the cycle (1, 1) -> (1, 2) -> (1, 1) is invalid because from (1, 2) we visited (1, 1) which was the last visited cell.

Return true if any cycle of the same value exists in grid, otherwise, return false.

 

Example 1:

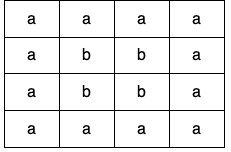
Input: grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
Output: true
Explanation: There are two valid cycles shown in different colors in the image below: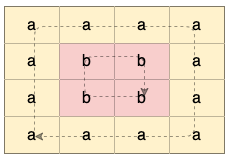

Example 2:

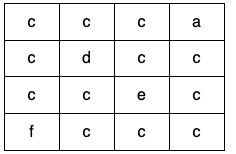
Input: grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
Output: true
Explanation: There is only one valid cycle highlighted in the image below: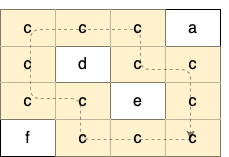

Example 3:

Input: grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
Output: false

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 500
  • grid consists only of lowercase English letters.

1559. Detect Cycles in 2D Grid

Problem Description

Given an m x n grid of characters, determine if there exists a cycle consisting of the same character. A cycle is a path of length 4 or more that starts and ends at the same cell, moving only to adjacent cells with the same character value, and avoiding immediate backtracking.

Solution Approach: Depth-First Search (DFS)

The most efficient approach to solve this problem is using Depth-First Search (DFS). We'll iterate through each cell of the grid. If a cell hasn't been visited, we initiate a DFS from that cell.

The DFS function needs to track:

  1. Current Cell Coordinates: (x, y)
  2. Previous Cell Coordinates: (px, py) (to prevent immediate backtracking)
  3. Visited Status: A 2D boolean array vis to mark visited cells.

During the DFS:

  • For each neighbor of the current cell, if the character matches and it's not the previous cell:
    • If the neighbor is already visited, we've found a cycle, return true.
    • Otherwise, recursively call DFS on the neighbor, updating the previous cell coordinates.
  • If no cycle is detected during the DFS from the current cell, return false.

After iterating through all cells and performing DFS where necessary, if no cycle is found, the function returns false.

Code Implementation (Python)

def containsCycle(grid):
    m, n = len(grid), len(grid[0])
    vis = [[False] * n for _ in range(m)]
    dirs = [(0, 1), (0, -1), (1, 0), (-1, 0)]  # Directions: Right, Left, Down, Up
 
    def dfs(x, y, px, py):
        vis[x][y] = True
        for dx, dy in dirs:
            nx, ny = x + dx, y + dy
            if 0 <= nx < m and 0 <= ny < n:
                if grid[nx][ny] == grid[x][y] and (nx != px or ny != py):
                    if vis[nx][ny]:
                        return True
                    if dfs(nx, ny, x, y):
                        return True
        return False
 
    for i in range(m):
        for j in range(n):
            if not vis[i][j]:
                if dfs(i, j, -1, -1):
                    return True
    return False

Time and Space Complexity Analysis

  • Time Complexity: O(m * n), where 'm' and 'n' are the dimensions of the grid. Each cell is visited at most once.
  • Space Complexity: O(m * n) due to the vis array used for tracking visited cells. The recursion depth in the worst case is also proportional to m * n.

Other Language Implementations

The solution can be implemented similarly in other languages like Java, C++, JavaScript, etc., with minor syntactic differences. The core logic of DFS with visited cell tracking remains the same. The key is to correctly manage the visited array and the traversal directions to avoid unnecessary computations.