{x}
blog image

Delete Node in a BST

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

  1. Search for a node to remove.
  2. If the node is found, delete the node.

 

Example 1:

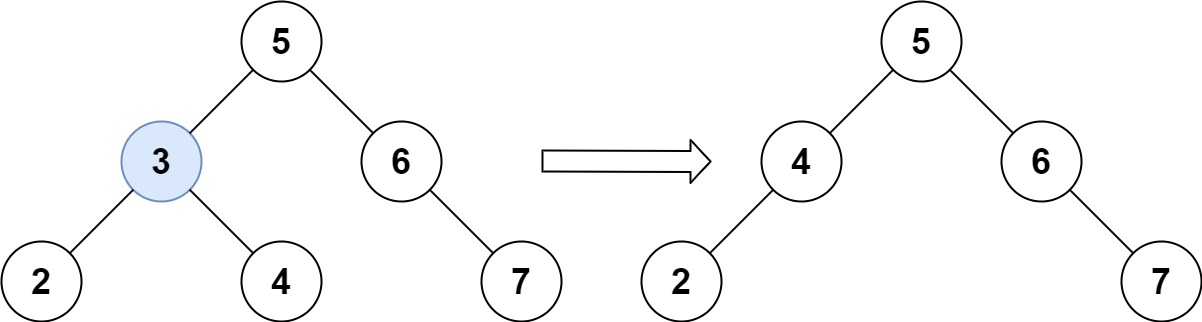
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.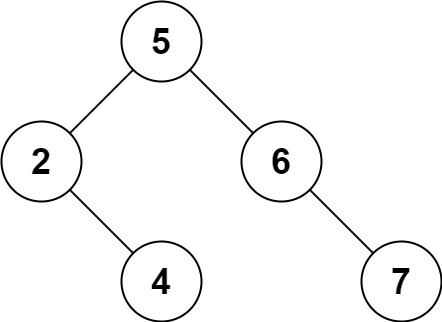

Example 2:

Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:

Input: root = [], key = 0
Output: []

 

Constraints:

  • The number of nodes in the tree is in the range [0, 104].
  • -105 <= Node.val <= 105
  • Each node has a unique value.
  • root is a valid binary search tree.
  • -105 <= key <= 105

 

Follow up: Could you solve it with time complexity O(height of tree)?

Solution Explanation: Deleting a Node in a BST

This problem involves deleting a node with a given key from a Binary Search Tree (BST). The solution employs a recursive approach with several cases to handle:

1. Base Case: If the root is null (empty tree), return null.

2. Recursive Search:

  • If the key is less than the current node's value, recursively call deleteNode on the left subtree.
  • If the key is greater than the current node's value, recursively call deleteNode on the right subtree.

3. Node Found (key == root.val):

This is where the deletion logic resides. There are three sub-cases:

  • Case A: Node is a leaf node (no children): Simply return null to remove the node.

  • Case B: Node has one child: Return the single child node to replace the node being deleted.

  • Case C: Node has two children: This is the most complex case. The solution employs the following strategy:

    • Find the inorder successor (smallest node in the right subtree). This is the node with the smallest value larger than the node being deleted. The code efficiently finds it by traversing the left-most node in the right subtree.
    • Copy the value of the inorder successor to the node being deleted.
    • Recursively delete the inorder successor (which is now a duplicate). This ensures that the BST property is maintained.

Time Complexity Analysis:

The time complexity is O(H), where H is the height of the BST. In the worst case (a skewed tree), H can be equal to N (the number of nodes), resulting in O(N) time complexity. In the best case (a balanced tree), H is log₂(N), leading to O(log₂(N)) time complexity. The recursive calls only traverse a path down the tree, hence the height dependency.

Space Complexity Analysis:

The space complexity is O(H) in the worst case due to the recursive call stack. Again, for a skewed tree, this becomes O(N), while for a balanced tree, it's O(log₂(N)).

Code Explanation (Python Example):

The Python code directly implements the algorithm described above:

class Solution:
    def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
        if root is None:  # Base case: empty tree
            return None
 
        if root.val > key:  # Recursive search on left subtree
            root.left = self.deleteNode(root.left, key)
            return root
        elif root.val < key: # Recursive search on right subtree
            root.right = self.deleteNode(root.right, key)
            return root
        else:  # Node found (key == root.val)
            if root.left is None: # Case A or B: One or zero children
                return root.right
            elif root.right is None:
                return root.left
            else:  # Case C: Two children
                node = root.right
                while node.left:  #Find inorder successor
                    node = node.left
                node.left = root.left  # Connect left subtree to successor
                root = root.right  # Replace the current node with its right subtree
                return root

The other languages (Java, C++, Go, TypeScript, Rust) follow the same logic, adapting the syntax and data structures specific to each language. The core algorithm remains consistent.