- {x}
- Online Election
- Sort an Array
- Cat and Mouse
- X of a Kind in a Deck of Cards
- Partition Array into Disjoint Intervals
- Word Subsets
- Reverse Only Letters
- Maximum Sum Circular Subarray
- Complete Binary Tree Inserter
- Number of Music Playlists
- Minimum Add to Make Parentheses Valid
- Sort Array By Parity II
- 3Sum With Multiplicity
- Minimize Malware Spread
- Long Pressed Name
- Flip String to Monotone Increasing
- Three Equal Parts
- Read More...

Complete Binary Tree Inserter
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the CBTInserter class:
CBTInserter(TreeNode root)Initializes the data structure with therootof the complete binary tree.int insert(int v)Inserts aTreeNodeinto the tree with valueNode.val == valso that the tree remains complete, and returns the value of the parent of the insertedTreeNode.TreeNode get_root()Returns the root node of the tree.
Example 1:
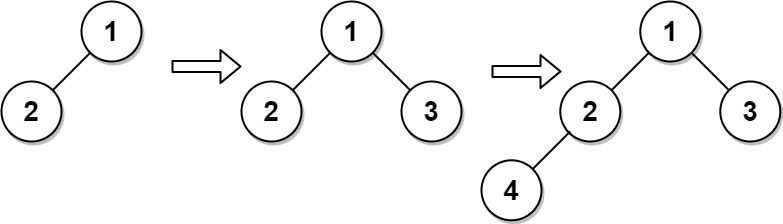
Input ["CBTInserter", "insert", "insert", "get_root"] [[[1, 2]], [3], [4], []] Output [null, 1, 2, [1, 2, 3, 4]] Explanation CBTInserter cBTInserter = new CBTInserter([1, 2]); cBTInserter.insert(3); // return 1 cBTInserter.insert(4); // return 2 cBTInserter.get_root(); // return [1, 2, 3, 4]
Constraints:
- The number of nodes in the tree will be in the range
[1, 1000]. 0 <= Node.val <= 5000rootis a complete binary tree.0 <= val <= 5000- At most
104calls will be made toinsertandget_root.
Solution Explanation: Complete Binary Tree Inserter
This problem involves designing a data structure and algorithms to efficiently insert nodes into a complete binary tree while maintaining its completeness. A complete binary tree is one where all levels are completely filled except possibly the last, and all nodes are as far left as possible.
The solution uses a Breadth-First Search (BFS) approach combined with an array-based representation of the tree. This allows for O(1) insertion and root retrieval.
Algorithm:
-
__init__(root)(Constructor):- Initializes a list
treeto store all nodes of the tree. - Performs a BFS traversal of the input
rootto populate thetreelist. Each node is added to the list in level-order (from left to right, level by level).
- Initializes a list
-
insert(val):- Finds the parent node
pof the new node to be inserted. Since the tree is complete, the parent of the last node is always at index(tree.length - 1) // 2. - Creates a new node
nodewith the givenval. - Adds
nodeto thetreelist. - Attaches
nodeas the left child ofpifp.leftisNone; otherwise, it attachesnodeas the right child ofp. - Returns the value of the parent node
p.
- Finds the parent node
-
get_root():- Returns the root node of the tree, which is always the first element in the
treelist (index 0).
- Returns the root node of the tree, which is always the first element in the
Time Complexity Analysis:
__init__(root): The BFS traversal takes O(N) time, where N is the number of nodes in the tree.insert(val): All operations within this function (finding the parent, creating the node, adding to the list, and attaching as a child) take O(1) time.get_root(): Retrieving the root node from the list takes O(1) time.
Space Complexity Analysis:
- The
treelist stores all nodes of the tree, so the space complexity is O(N).
Code Implementation (Python):
from collections import deque
from typing import Optional
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class CBTInserter:
def __init__(self, root: Optional[TreeNode]):
self.tree = []
q = deque([root])
while q:
for _ in range(len(q)):
node = q.popleft()
self.tree.append(node)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
def insert(self, val: int) -> int:
p = self.tree[(len(self.tree) - 1) // 2]
node = TreeNode(val)
self.tree.append(node)
if p.left is None:
p.left = node
else:
p.right = node
return p.val
def get_root(self) -> Optional[TreeNode]:
return self.tree[0]The implementations in other languages (Java, C++, Go, TypeScript, JavaScript) follow the same algorithmic structure, differing only in syntax and data structure specifics. They all achieve the same time and space complexities.