{x}
blog image

Check if Move is Legal

You are given a 0-indexed 8 x 8 grid board, where board[r][c] represents the cell (r, c) on a game board. On the board, free cells are represented by '.', white cells are represented by 'W', and black cells are represented by 'B'.

Each move in this game consists of choosing a free cell and changing it to the color you are playing as (either white or black). However, a move is only legal if, after changing it, the cell becomes the endpoint of a good line (horizontal, vertical, or diagonal).

A good line is a line of three or more cells (including the endpoints) where the endpoints of the line are one color, and the remaining cells in the middle are the opposite color (no cells in the line are free). You can find examples for good lines in the figure below:

Given two integers rMove and cMove and a character color representing the color you are playing as (white or black), return true if changing cell (rMove, cMove) to color color is a legal move, or false if it is not legal.

 

Example 1:

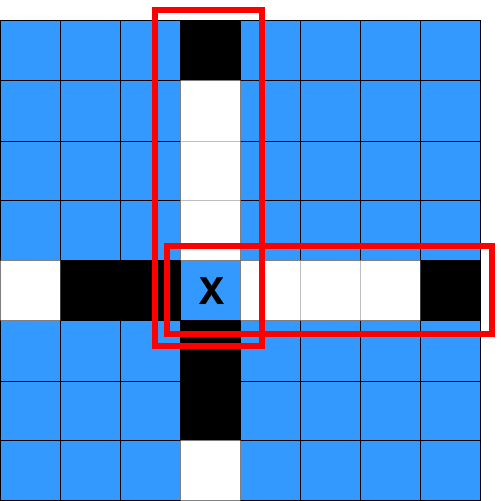
Input: board = [[".",".",".","B",".",".",".","."],[".",".",".","W",".",".",".","."],[".",".",".","W",".",".",".","."],[".",".",".","W",".",".",".","."],["W","B","B",".","W","W","W","B"],[".",".",".","B",".",".",".","."],[".",".",".","B",".",".",".","."],[".",".",".","W",".",".",".","."]], rMove = 4, cMove = 3, color = "B"
Output: true
Explanation: '.', 'W', and 'B' are represented by the colors blue, white, and black respectively, and cell (rMove, cMove) is marked with an 'X'.
The two good lines with the chosen cell as an endpoint are annotated above with the red rectangles.

Example 2:

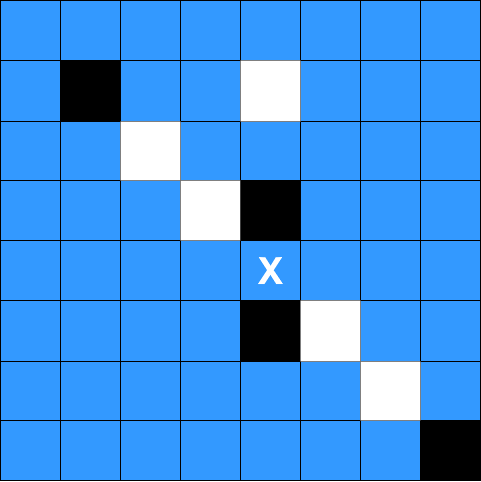
Input: board = [[".",".",".",".",".",".",".","."],[".","B",".",".","W",".",".","."],[".",".","W",".",".",".",".","."],[".",".",".","W","B",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".","B","W",".","."],[".",".",".",".",".",".","W","."],[".",".",".",".",".",".",".","B"]], rMove = 4, cMove = 4, color = "W"
Output: false
Explanation: While there are good lines with the chosen cell as a middle cell, there are no good lines with the chosen cell as an endpoint.

 

Constraints:

  • board.length == board[r].length == 8
  • 0 <= rMove, cMove < 8
  • board[rMove][cMove] == '.'
  • color is either 'B' or 'W'.

This problem requires determining if placing a piece of a certain color (color) at a given location (rMove, cMove) on a chessboard (board) creates a "good line". A good line consists of three or more consecutive pieces where the endpoints are the same color and the inner pieces are the opposite color.

Approach

The solution employs a straightforward approach of checking all eight directions (up, down, left, right, and four diagonals) from the given cell. For each direction, it iterates along the line until it encounters a cell that's either empty (.) or of the same color as the placed piece. It counts the consecutive pieces of the opposite color encountered. If the count of opposite-colored pieces is greater than 1 (implying at least 3 pieces in total, with 2 opposite color and 1 same color at the end), and the final piece encountered is the same color as the placed piece, a "good line" is found, and the function returns true.

If no such good line is found after checking all directions, the function returns false.

Time Complexity Analysis

The algorithm iterates through at most 8 directions. In each direction, it traverses at most 7 cells (since it's an 8x8 board and we only check up to the edge). Therefore, the maximum number of cells visited is 8 * 7 = 56. This makes the time complexity O(1) because it's a constant number of operations regardless of the board size (in this specific case, an 8x8 board). While the board could be of any size n x n, the problem statement strictly specifies an 8x8 board, hence the constant time complexity.

Space Complexity Analysis

The algorithm uses a constant amount of extra space to store variables like a, b, i, j, and cnt. Thus, the space complexity is O(1), which is constant.

Code Implementation (Python)

class Solution:
    def checkMove(self, board: List[List[str]], rMove: int, cMove: int, color: str) -> bool:
        for a in range(-1, 2):
            for b in range(-1, 2):
                if a == 0 and b == 0:
                    continue
                i, j = rMove, cMove
                cnt = 0
                while 0 <= i + a < 8 and 0 <= j + b < 8:
                    cnt += 1
                    i, j = i + a, j + b
                    if cnt > 1 and board[i][j] == color:
                        return True
                    if board[i][j] in (color, "."):
                        break
        return False

The code for other languages (Java, C++, Go, TypeScript) follows a similar structure and logic, differing only in syntax and specific library functions. The core algorithm remains the same, guaranteeing the same time and space complexities.