- {x}
- Minimum Genetic Mutation
- Number of Segments in a String
- Non-overlapping Intervals
- Find Right Interval
- Path Sum III
- Find All Anagrams in a String
- Ternary Expression Parser
- K-th Smallest in Lexicographical Order
- Arranging Coins
- Find All Duplicates in an Array
- String Compression
- Sequence Reconstruction
- Add Two Numbers II
- Arithmetic Slices II - Subsequence
- Number of Boomerangs
- Find All Numbers Disappeared in an Array
- Serialize and Deserialize BST
- Read More...

Arranging Coins
You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.
Given the integer n, return the number of complete rows of the staircase you will build.
Example 1:
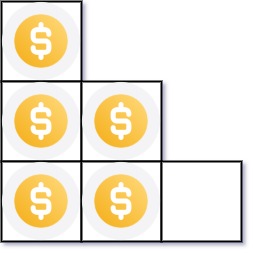
Input: n = 5 Output: 2 Explanation: Because the 3rd row is incomplete, we return 2.
Example 2:
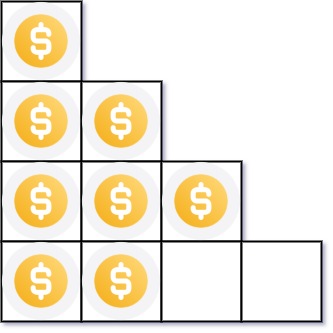
Input: n = 8 Output: 3 Explanation: Because the 4th row is incomplete, we return 3.
Constraints:
1 <= n <= 231 - 1
Solution Explanation for Arranging Coins
The problem asks to find the number of complete rows in a staircase built using n coins, where each row i contains i coins. This translates to finding the largest integer k such that the sum of integers from 1 to k (1 + 2 + ... + k) is less than or equal to n. The sum of integers from 1 to k is given by the formula k(k+1)/2.
Approach 1: Mathematical Formula
The problem can be solved directly using a mathematical formula derived from the arithmetic series sum. We need to solve the inequality k(k+1)/2 ≤ n for k. This leads to a quadratic equation, which can be solved using the quadratic formula. However, a simpler approximation can be used: k ≈ √(2n). We need to adjust this slightly for accuracy.
Time Complexity: O(1) - Constant time because it involves a single calculation. Space Complexity: O(1) - Constant space because it uses a fixed number of variables.
Code:
(Python3, Java, and C++ code provided in the original response demonstrate this approach)
Approach 2: Binary Search
Since we are looking for the largest integer k satisfying k(k+1)/2 ≤ n, we can use binary search to efficiently find this value. The search space is from 1 to n.
Time Complexity: O(log n) - Logarithmic time due to binary search. Space Complexity: O(1) - Constant space because it uses a fixed number of variables.
Code:
(Python3 and Java code provided in the original response demonstrate this approach. The C++ and Go versions in the original response also use a slightly modified binary search.)
Detailed Explanation of Binary Search Approach (using Python):
class Solution:
def arrangeCoins(self, n: int) -> int:
left, right = 1, n # Initialize search space
while left < right: # Continue until left and right pointers meet
mid = (left + right + 1) // 2 # Calculate the middle point (rounding up)
if (1 + mid) * mid // 2 <= n: # Check if sum up to mid is <= n
left = mid # If true, mid could be a solution, so update left pointer
else:
right = mid - 1 # If false, mid is too large, update right pointer
return left # Return the final value of left (the largest k)The binary search efficiently narrows down the search space by half in each iteration. The (left + right + 1) // 2 ensures that if mid is a valid solution, the search continues on the right side, aiming to find a potentially larger solution. The floor division // is used to ensure integer division.
In summary, both approaches solve the problem, but the binary search offers a more efficient solution for larger values of n due to its logarithmic time complexity compared to the constant time (but potentially less precise) mathematical approach. The mathematical approach is faster for smaller values of n but may be subject to precision limitations with floating point calculations.