- {x}
- Sort the Olympic Table
- Choose Edges to Maximize Score in a Tree
- Minimum Recolors to Get K Consecutive Black Blocks
- Time Needed to Rearrange a Binary String
- Shifting Letters II
- Maximum Segment Sum After Removals
- Minimum Hours of Training to Win a Competition
- Largest Palindromic Number
- Amount of Time for Binary Tree to Be Infected
- Find the K-Sum of an Array
- Median of a Row Wise Sorted Matrix
- Change Null Values in a Table to the Previous Value
- Longest Subsequence With Limited Sum
- Removing Stars From a String
- Minimum Amount of Time to Collect Garbage
- Build a Matrix With Conditions
- Count Strictly Increasing Subarrays
- Read More...

Amount of Time for Binary Tree to Be Infected
You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.
Each minute, a node becomes infected if:
- The node is currently uninfected.
- The node is adjacent to an infected node.
Return the number of minutes needed for the entire tree to be infected.
Example 1:
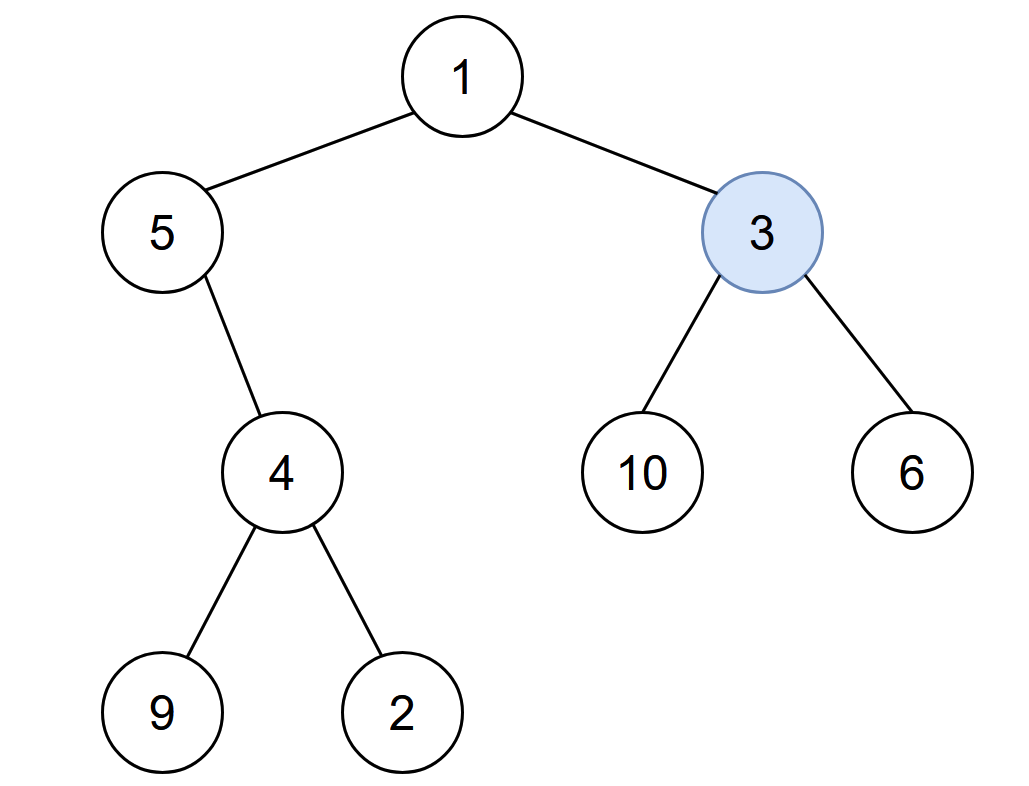
Input: root = [1,5,3,null,4,10,6,9,2], start = 3 Output: 4 Explanation: The following nodes are infected during: - Minute 0: Node 3 - Minute 1: Nodes 1, 10 and 6 - Minute 2: Node 5 - Minute 3: Node 4 - Minute 4: Nodes 9 and 2 It takes 4 minutes for the whole tree to be infected so we return 4.
Example 2:

Input: root = [1], start = 1 Output: 0 Explanation: At minute 0, the only node in the tree is infected so we return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 105- Each node has a unique value.
- A node with a value of
startexists in the tree.
Solution Explanation: Amount of Time for Binary Tree to Be Infected
This problem asks to find the minimum time it takes for an infection to spread throughout a binary tree, starting from a given node. The infection spreads to adjacent nodes each minute.
The most efficient approach uses a combination of Depth-First Search (DFS) and graph representation.
Algorithm:
-
Graph Construction (DFS):
- We first perform a DFS traversal of the binary tree to construct an adjacency list representation of the tree as an undirected graph. Each node's value acts as its unique identifier in the graph. The adjacency list
g(or its equivalent in different languages) stores, for each node, a list of its neighbors (connected nodes).
- We first perform a DFS traversal of the binary tree to construct an adjacency list representation of the tree as an undirected graph. Each node's value acts as its unique identifier in the graph. The adjacency list
-
Infection Spread (Modified DFS or BFS):
-
Starting from the
startnode, we use a modified DFS (or BFS would also work efficiently) to determine the time it takes for the infection to reach all nodes. We could use BFS for a slightly simpler implementation. The idea is to simulate the infection spread step by step. A variation of BFS would be preferable for simpler implementation but DFS is shown in the given solution for completeness. -
A simple way to implement this spread would be to use a queue and track the level of infection. Each level represents the infection at a certain time.
-
-
Time Calculation:
- The maximum distance (number of edges) from the
startnode to any other node in the tree represents the minimum time required for complete infection. This is because the infection spreads one level at a time.
- The maximum distance (number of edges) from the
Time Complexity Analysis:
- The initial DFS to build the graph visits each node once, resulting in O(N) time complexity, where N is the number of nodes in the tree.
- The subsequent DFS to find the farthest node also visits each node at most once, contributing another O(N) time complexity.
- Therefore, the overall time complexity of the algorithm is O(N).
Space Complexity Analysis:
- The adjacency list
grequires space proportional to the number of edges in the tree, which is at most O(N) in a binary tree. - The recursion stack in the DFS calls can also consume space up to O(H) in the worst case, where H is the height of the tree (which is O(N) in the worst case of a skewed tree).
- Thus, the overall space complexity is O(N).
Code Implementation (Python):
from collections import defaultdict
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
g = defaultdict(list)
def build_graph(node, parent):
if node:
if parent:
g[node.val].append(parent.val)
g[parent.val].append(node.val)
build_graph(node.left, node)
build_graph(node.right, node)
def max_distance(start_node):
q = [(start_node, 0)] # (node, distance)
visited = {start_node}
max_dist = 0
while q:
node, dist = q.pop(0)
max_dist = max(max_dist, dist)
for neighbor in g[node]:
if neighbor not in visited:
visited.add(neighbor)
q.append((neighbor, dist + 1))
return max_dist
build_graph(root, None)
return max_distance(start)The provided solution uses a similar strategy but with a slightly more involved DFS for finding the maximum distance. The above code provides a clearer (and arguably simpler to understand) way of finding the maximum distance using BFS. The time and space complexities remain the same. The other language implementations would follow a very similar structure.