{x}
blog image

Minimum Obstacle Removal to Reach Corner

You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:

  • 0 represents an empty cell,
  • 1 represents an obstacle that may be removed.

You can move up, down, left, or right from and to an empty cell.

Return the minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1).

 

Example 1:

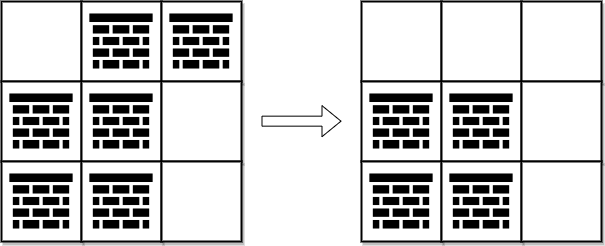
Input: grid = [[0,1,1],[1,1,0],[1,1,0]]
Output: 2
Explanation: We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
It can be shown that we need to remove at least 2 obstacles, so we return 2.
Note that there may be other ways to remove 2 obstacles to create a path.

Example 2:

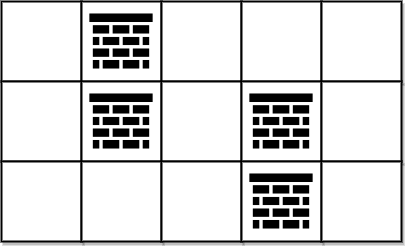
Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
Output: 0
Explanation: We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 105
  • 2 <= m * n <= 105
  • grid[i][j] is either 0 or 1.
  • grid[0][0] == grid[m - 1][n - 1] == 0

Minimum Obstacle Removal to Reach Corner

This problem asks for the minimum number of obstacles to remove to reach the bottom-right corner from the top-left corner in a grid. We can solve this using a breadth-first search (BFS) algorithm, prioritizing cells with fewer obstacles removed.

Approach

  1. Initialization:

    • We start at (0, 0) with 0 obstacles removed.
    • We use a deque (double-ended queue) to store cells to visit, prioritizing cells with fewer removed obstacles.
    • We use a visited set to track visited cells to avoid cycles.

  2. BFS Traversal:

    • We repeatedly dequeue a cell (i, j) and its associated obstacle count k.
    • If (i, j) is the target cell (m-1, n-1), we've found the solution, so return k.
    • If (i, j) has already been visited, skip it.
    • Mark (i, j) as visited.
    • Explore the four neighboring cells:
      • If a neighbor is empty (0), add it to the front of the deque (higher priority).
      • If a neighbor is an obstacle (1), add it to the back of the deque (lower priority), incrementing the obstacle count k.

  3. Time and Space Complexity:

    • Time Complexity: O(mn), where 'm' and 'n' are the dimensions of the grid. In the worst case, we visit each cell once.
    • Space Complexity: O(mn) in the worst case, as the deque and visited set can store all the cells.

Code (Python)

from collections import deque
 
class Solution:
    def minimumObstacles(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        q = deque([(0, 0, 0)]) # (row, col, obstacles removed)
        visited = set()
        dirs = [(0, 1), (0, -1), (1, 0), (-1, 0)] # directions
 
        while q:
            row, col, obstacles = q.popleft()
            if (row, col) == (m - 1, n - 1):
                return obstacles
            if (row, col) in visited:
                continue
            visited.add((row, col))
 
            for dr, dc in dirs:
                new_row, new_col = row + dr, col + dc
                if 0 <= new_row < m and 0 <= new_col < n:
                    if grid[new_row][new_col] == 0: # empty cell, higher priority
                        q.appendleft((new_row, new_col, obstacles))
                    else: # obstacle, lower priority
                        q.append((new_row, new_col, obstacles + 1))

The code in other languages (Java, C++, Go, TypeScript) follows the same logic, using appropriate data structures for the deque and visited set. The core algorithm remains a breadth-first search prioritizing cells based on the number of obstacles encountered.