- {x}
- Maximum Total Importance of Roads
- Booking Concert Tickets in Groups
- Rearrange Characters to Make Target String
- Apply Discount to Prices
- Steps to Make Array Non-decreasing
- Minimum Obstacle Removal to Reach Corner
- Maximum Profit From Trading Stocks
- Products With Three or More Orders in Two Consecutive Years
- Min Max Game
- Partition Array Such That Maximum Difference Is K
- Replace Elements in an Array
- Design a Text Editor
- Jump Game VIII
- Tasks Count in the Weekend
- Strong Password Checker II
- Successful Pairs of Spells and Potions
- Match Substring After Replacement
- Read More...

Min Max Game
You are given a 0-indexed integer array nums whose length is a power of 2.
Apply the following algorithm on nums:
- Let
nbe the length ofnums. Ifn == 1, end the process. Otherwise, create a new 0-indexed integer arraynewNumsof lengthn / 2. - For every even index
iwhere0 <= i < n / 2, assign the value ofnewNums[i]asmin(nums[2 * i], nums[2 * i + 1]). - For every odd index
iwhere0 <= i < n / 2, assign the value ofnewNums[i]asmax(nums[2 * i], nums[2 * i + 1]). - Replace the array
numswithnewNums. - Repeat the entire process starting from step 1.
Return the last number that remains in nums after applying the algorithm.
Example 1:
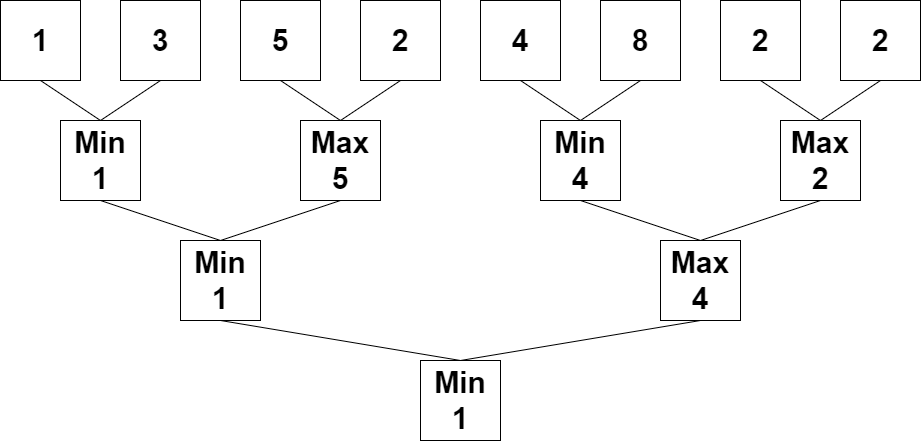
Input: nums = [1,3,5,2,4,8,2,2] Output: 1 Explanation: The following arrays are the results of applying the algorithm repeatedly. First: nums = [1,5,4,2] Second: nums = [1,4] Third: nums = [1] 1 is the last remaining number, so we return 1.
Example 2:
Input: nums = [3] Output: 3 Explanation: 3 is already the last remaining number, so we return 3.
Constraints:
1 <= nums.length <= 10241 <= nums[i] <= 109nums.lengthis a power of2.
Solution Explanation: Min Max Game
The problem describes an iterative process applied to an array of numbers where the length is always a power of 2. The process repeatedly shrinks the array by half, applying min or max operations based on the index. The goal is to find the single remaining number after this process completes.
Approach:
The most straightforward approach is to simulate the algorithm directly. We iterate until the array has only one element. In each iteration:
- Reduce Array Size: The new array size is half the previous size (
n >>= 1orn = n / 2). - Iterate and Apply Operations: We iterate through the new array's indices (0 to
n-1). For each indexi:- If
iis even, we take theminof the corresponding pair of elements from the previous array (nums[2*i]andnums[2*i + 1]). - If
iis odd, we take themaxof the corresponding pair.
- If
- Update Array: The calculated
minormaxvalues are stored back into the originalnumsarray, effectively replacing the older elements. - Repeat: Steps 1-3 are repeated until only one element remains.
Time and Space Complexity:
-
Time Complexity: The algorithm iterates through the array roughly
log₂(n)times (wherenis the initial array length), with each iteration processingn/2,n/4,n/8, ... elements. The total number of operations is approximatelyn + n/2 + n/4 + ... ≈ 2n, which simplifies to O(n). -
Space Complexity: The algorithm modifies the input array in place; therefore, it uses constant extra space, O(1). No auxiliary data structures are used proportionally to the input size.
Code Implementation (Python):
class Solution:
def minMaxGame(self, nums: List[int]) -> int:
n = len(nums)
while n > 1:
n >>= 1 # n //= 2 (Integer division)
new_nums = []
for i in range(n):
if i % 2 == 0:
new_nums.append(min(nums[2 * i], nums[2 * i + 1]))
else:
new_nums.append(max(nums[2 * i], nums[2 * i + 1]))
nums = new_nums # Replace the old array
return nums[0]Improvements in other language examples:
The provided solutions in other languages (Java, C++, Go, etc.) optimize the space complexity further by directly modifying the original nums array instead of creating a new new_nums array in each iteration. This makes the code more efficient and concise. The bitwise operations (i << 1, i << 1 | 1) are used as a faster way to calculate 2 * i and 2 * i + 1.
The core logic remains the same across all languages—simulate the algorithm step-by-step until a single element is left. The choice of language affects mainly the syntax and minor efficiency details.